Question

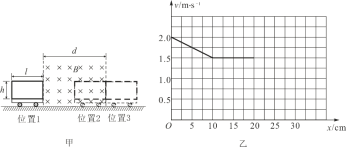
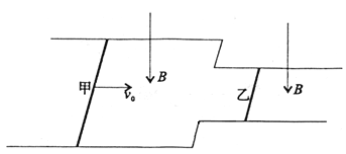
【题目】如图所示，宽度为2d与宽度为d的两部分导轨衔接良好固定在水平面上，整个空间存在竖直向下的匀强磁场，磁感应强度大小为B，长度分别为2d和d的导体棒甲和乙按如图的方式置于导轨上，已知两导体棒的质量均为m、两导体棒单位长度的电阻均为r0，现给导体棒甲以水平向右的初速度v0。假设导轨的电阻忽略不计、导体棒与导轨之间的摩擦可忽略不计，且两部分导轨足够长。求：

(1)当导体棒甲开始运动瞬间，甲、乙两棒的加速度大小分别为多大？

(2)导体棒甲匀速时的速度大小应为多大？

(3)两导体棒从开始运动到刚匀速的过程中两导体棒发生的位移分别是x甲和x乙，试写出两导体棒的位移x甲和x乙之间的关系式。

Answer 1

【答案】(1)、(2)v0 (3)

【解析】

现给导体棒甲以水平向右的初速度v0可知，本题考查电磁感应现象中的动力学问题，根据法拉第的电磁感应定律与闭合电路欧姆定律综合牛顿运动定律进行求解。

(1) 导体棒甲刚开始运动时电源电动势为E＝2Bdv0

由题意整个电路的总电阻为

由闭合电路的欧姆定律，电路中的总电流大小为

由以上整理可得导体棒甲、乙所受的安培力大小分别为 ，

由牛顿第二定律可知导体棒甲、乙的加速度大小分别为 ，；

(2) 由动量定理，对导体棒甲有

即：

同理对导体棒乙有

两导体棒均匀速运动时，有v2＝2v1

联立以上可解得；

(3)由得

由法拉第电磁感应定律得

又

整理得：

联立以上可得