题目内容
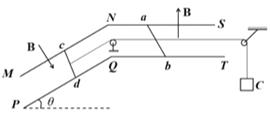
【题目】如图所示,在倾斜角为30°的光滑斜面上静止放置![]() 、
、![]() 两个小球,它们的质量分别为
两个小球,它们的质量分别为![]() 和
和![]() ,它们的半径分别为
,它们的半径分别为![]() 和
和![]() ,它们之间用长为
,它们之间用长为![]() 的轻绳相连(图中未画出),开始时
的轻绳相连(图中未画出),开始时![]() 、
、![]() 紧靠在一起并锁定于斜面上的
紧靠在一起并锁定于斜面上的![]() 处,在斜面上的
处,在斜面上的![]() 处固定一个开有小孔的挡板,小孔半径为
处固定一个开有小孔的挡板,小孔半径为![]() ,
,![]() 间距离为
间距离为![]() ,现解除对小球的锁定,让
,现解除对小球的锁定,让![]() 、
、![]() 一起从静止开始沿斜面下滑,
一起从静止开始沿斜面下滑,![]() 球无阻碍地通过小孔,而
球无阻碍地通过小孔,而![]() 球与挡板发生无机械能损失的碰撞,
球与挡板发生无机械能损失的碰撞,![]() 球碰撞后沿斜面向上运动,
球碰撞后沿斜面向上运动,![]() 球仍沿斜面向下运动,轻绳绷紧瞬间(时间极短)两球达到共同速度
球仍沿斜面向下运动,轻绳绷紧瞬间(时间极短)两球达到共同速度![]() ,已知两球半径远小于轻绳长度
,已知两球半径远小于轻绳长度![]() ,在计算时将
,在计算时将![]() 、
、![]() 两球看做质点,斜面足够长,两小球始终在斜面上运动,
两球看做质点,斜面足够长,两小球始终在斜面上运动,![]() 取
取![]() ,求:
,求:
(1)小球![]() 、
、![]() 从
从![]() 点由静止开始一起沿斜面下滑到达挡板时的速度
点由静止开始一起沿斜面下滑到达挡板时的速度![]() 的大小;
的大小;
(2)若![]() ,连接
,连接![]() 、
、![]() 两球的轻绳绷紧瞬间,
两球的轻绳绷紧瞬间,![]() 、
、![]() 两球共同速度
两球共同速度![]() 的大小和方向;
的大小和方向;
(3)若![]() ,试讨论两球共同速度
,试讨论两球共同速度![]() 的方向与
的方向与![]() 值的关系。
值的关系。
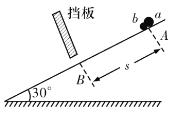
【答案】(1)5m/s;(2)![]() ,方向沿斜面向下;(3)见解析
,方向沿斜面向下;(3)见解析
【解析】
(1)![]() 一起下滑时根据动能定理有
一起下滑时根据动能定理有
![]()
代入数据得![]() ;
;
(2)![]() 与挡板发生碰撞反弹到绳刚好绷紧,根据受力分析可知两球的加速度为
与挡板发生碰撞反弹到绳刚好绷紧,根据受力分析可知两球的加速度为![]() ,则有
,则有
![]()
这段过程中![]() 球的位移
球的位移
![]()
![]() 球的位移
球的位移
![]()
又因为
![]()
代入数据解得![]() ;绳绷紧前瞬间有
;绳绷紧前瞬间有
![]()
![]()
绳绷紧过程动量守恒,取斜面向下为正,有
![]()
当![]() 时解得
时解得![]() ;故绳绷紧瞬间,
;故绳绷紧瞬间,![]() 、
、![]() 两球的共同速度
两球的共同速度![]() 的大小为
的大小为![]() ,方向沿斜面向下;
,方向沿斜面向下;
(3)若
![]()
由(2)问可得
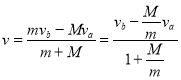
令![]() ,可得
,可得![]() ,则讨论当
,则讨论当![]() 时,
时,![]() ,方向沿斜面向下;当
,方向沿斜面向下;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,方向沿斜面向上。
,方向沿斜面向上。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目