题目内容
【题目】如图所示,相距L=0.5m的平行导轨MNS、PQT处在磁感应强度B=0.4T的匀强磁场中,水平导轨处的磁场方向竖直向上,光滑倾斜导轨处的磁场方向垂直于导轨平面斜向下。质量均为m=0.04kg、电阻均为R=0.1Ω的导体棒ab、cd均垂直放置于导轨上,并与导轨接触良好,导轨电阻不计。质量为M=0.20kg的物体C,用绝缘细线绕过光滑的定滑轮分别与导体棒ab、cd相连接。细线沿导轨中心线且在导轨平面内,细线及滑轮质量不计。已知倾斜导轨与水平面的夹角![]() =37°,水平导轨与ab棒间的动摩擦因数μ=0.4。重力加速度g=10m/s2,水平导轨足够长,导体棒cd运动过程中始终不离开倾斜导轨。物体C由静止释放,当它达到最大速度时下落高度h=1m,求这一运动过程中:(sin37°=0.6,cos37°=0.8)
=37°,水平导轨与ab棒间的动摩擦因数μ=0.4。重力加速度g=10m/s2,水平导轨足够长,导体棒cd运动过程中始终不离开倾斜导轨。物体C由静止释放,当它达到最大速度时下落高度h=1m,求这一运动过程中:(sin37°=0.6,cos37°=0.8)
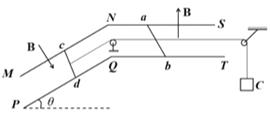
(1)物体C能达到的最大速度![]() 是多少?
是多少?
(2)由于摩擦产生的内能与电流产生的内能各为多少?
(3)若当棒ab、cd达到最大速度的瞬间,连接导体棒ab、cd及物体C的绝缘细线突然同时断裂,且ab棒也刚好进入到水平导轨的更加粗糙部分(ab棒与水平导轨间的动摩擦因数变为![]() =0.6)。若从绝缘细线断裂到ab棒速度减小为零的过程中ab棒向右发生的位移x=0.11m,求这一过程所经历的时间?
=0.6)。若从绝缘细线断裂到ab棒速度减小为零的过程中ab棒向右发生的位移x=0.11m,求这一过程所经历的时间?
【答案】(1)2m/s (2)0.16J 1.04J (3)0.15s
【解析】
(1)设C达到最大速度为![]() ,由法拉第电磁感应定律可得回路的感应电动势为:
,由法拉第电磁感应定律可得回路的感应电动势为:
E=2BLvm ①
由欧姆定律可得回路中的电流强度为:![]() ②
②
金属导体棒ab、cd受到的安培力为:![]() ③
③
线中张力为T2,导体棒ab、cd及物体C的受力如图,
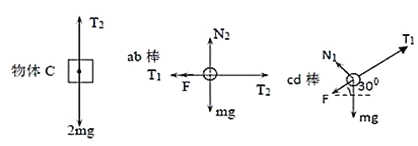
由平衡条件可得:![]() ,
,![]() ,
,![]() ④
④
联立①②③④解得![]() ⑤
⑤
(2)运动过程中由于摩擦产生的内能:E1=μmgh=0.16J ⑥
由能的转化和守恒定律可得:
![]() ⑦
⑦
联立⑤⑥⑦
将![]() ,代入可得这一过程由电流产生的内能:
,代入可得这一过程由电流产生的内能:![]()
(3)经分析, 在ab棒向右减速运动的过程中,其加速度大小与cd棒沿斜面向上运动的加速度大小始终相等,速率也始终相等。设某时刻它们的速率为v,则:E=2BLV
由欧姆定律可得回路中的电流强度为:![]()
金属导体棒ab、cd受到的安培力为:![]()
对ab棒运用动量定理: ![]()
又![]()
计算可得 t=0.15s

【题目】某同学用伏安法测一节干电池的电动势和内阻,现备有下列器材:
A.被测干电池一节 |
B.电流表:量程0~0.6A,内阻0.1Ω |
C.电流表:量程0~3A,内阻0.024Ω |
D.电压表:量程0~3V,内阻未知 |
E.电压表:量程0~15V,内阻未知
F.滑动变阻器:0~10Ω,2A
G.滑动变阻器:0~100Ω,1A
H.开关、导线若干
在伏安法测电池电动势和内阻的实验中,由于电流表和电压表内阻的影响,测量结果存在系统误差.在现有器材的条件下,要尽可能准确地测量电池的电动势和内阻.
(1)在上述器材中请选择适当的器材:____ ____(填写选项前的字母);
(2)在图方框中画出相应的实验电路图;
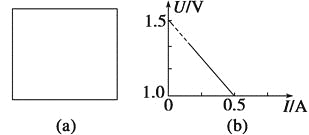
(3)根据实验中电流表和电压表的示数得到了如图所示的U-I图象,则在修正了实验系统误差后,干电池的电动势E=________V,内电阻r=________Ω.