Question

【题目】如图所示，一半径r = 0．2m的1/4光滑圆弧形槽底端B与水平传带相接，传送带的运行速度为v0=4m/s，长为L=1．25m , 滑块与传送带间的动摩擦因数μ=0．2,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管，EF段被弯成以O为圆心、半径R = 0．25m的一小段圆弧，管的D端弯成与水平传带C端平滑相接，O点位于地面，OF 连线竖直。一质量为m=0．2kg的物块a从圆弧顶端A点无初速滑下，滑到传送带上后做匀加速运动，然后滑块被传送带送入管DEF。已知a物块可视为质点，a的横截面略小于管中空部分的横截面，重力加速度g取10m/s2．求：

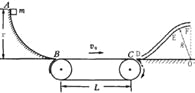
（1）滑块a到达底端B时的速度vB；

（2）滑块a刚到达管顶F点时对管壁的压力；

Answer 1

【答案】（1）2m/s（2）1．2N

【解析】试题分析：（1）设滑块到达B点的速度为vB，由机械能守恒定律，有

解得：vB=2m/s

（2）滑块在传送带上做匀加速运动，受到传送带对它的滑动摩擦力，

由牛顿第二定律μMg =Ma

滑块对地位移为L，末速度为vC，设滑块在传送带上一直加速

由速度位移关系式2Al=vC2-vB2

得vC=3m/s<4m/s，可知滑块与传送带未达共速 ,滑块从C至F，由机械能守恒定律，有

得vF=2m/s

在F处由牛顿第二定律

得FN=1．2N 由牛顿第三定律得管上壁受压力为1．2N, 压力方向竖直向上