题目内容
【题目】如图，两带电平行板长度和板间距离均为d，板间电压为u0，平行板右侧存在一直径为d的圆形匀强磁场区域，磁场方向垂直纸面向里。一个带正电的粒子以速度v0从平行板左侧飞入电场，速度方向垂直于板间电场的方向。粒子离开电场后从M点进入磁场，经N点离开磁场，MN为圆形磁场区域的一条直径，与水平成30°角。已知带电粒子的比荷满足
求：
(1)粒子离开电场时的速度方向与水平方向间的夹角；
(2)匀强磁场的磁感应强度B。
【答案】(1)300 (2)
【解析】
粒子在电场里做平抛运动，根据类平抛公式和速度关系即可求出粒子离开电场时的速度方向与水平方向间的夹角；画出粒子轨迹根据几何关系和牛顿第二定相结合即可求出匀强磁场的磁感应强度。
(1)粒子在电场里运动的时间为：
板间的场强为：
根据牛顿第二定律有：
竖直方向速度为：
粒子离开电场时的速度方向与水平方向间的夹角的正切值为：
联立以上可得：
（2）粒子运动轨迹如图所示：
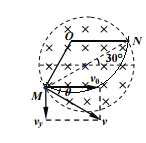
由几何关系：
根据速度关系：
根据牛顿第二定律：
联立解得：
练习册系列答案
相关题目
