题目内容
8.用轻绳拴一个质量为m的小球以v0匀速上升,现使拉力突然减小,并保持大小不变,直到小球速度减为零,设该过程中小球的加速度和位移大小分别为a和s,则拉力对小球做的功为( )| A. | $\frac{1}{2}$mv02 | B. | m(g+a)s | C. | mas | D. | m(g-a)s |
分析 根据牛顿第二定律求出拉力大小,再根据W=Fs即可求解拉力对小球做的功.也可以根据动能定理求出拉力做功.
解答 解:A、设拉力对小球做的功为W.根据动能定理得:W-mgs=0-$\frac{1}{2}m{v}_{0}^{2}$,得 W=mgs-$\frac{1}{2}m{v}_{0}^{2}$,故A错误.
BCD、根据牛顿第二定律得:mg-F=ma
解得:F=m(g-a)
则拉力对小球做的功 W=Fs=m(g-a)s,故BC错误,D正确.
故选:D
点评 解决本题的关键要掌握两种求功的方法:一是功的计算公式W=Fs.二是动能定理.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
18.下列说法中正确的( )
| A. | 第二类永动机和第一类永动机一样,都违背了能量守恒定律,因此不可能制成 | |
| B. | 根据能量守恒定律,经过不断的技术改造,热机的效率可以达到100% | |
| C. | 因为能量守恒,所以“能源危机”是不可能真正出现的 | |
| D. | 自然界中的能量是守恒的,但有的能量便于利用,有的不便于利用,因此要节约能源 |
19.某人沿着半径为 R的水平圆周跑道跑了1.75圈时,他的( )
| A. | 路程和位移的大小均为3.5πR | |
| B. | 路程和位移的大小均为$\sqrt{2}$R | |
| C. | 路程为3.5πR、位移的大小为$\sqrt{2}$R | |
| D. | 平均速率是平均速度大小的1.75$\sqrt{2}$π倍 |
3.一小孩从公园中的滑梯上匀速滑下,下列关于小孩的机械能变化说法中正确的是( )
| A. | 重力势能减小,机械能减小 | B. | 重力势能减小,机械能不变 | ||
| C. | 重力势能不变,机械能减小 | D. | 重力势能不变,机械能增加 |
13.对以a=5m/s2作匀加速直线运动的物体,下列说法正确的是( )
| A. | 在任意1s的末速度比初速度大5m/s | |
| B. | 第2s初的速度比第1s末的速度大5m/s | |
| C. | 任意1s末的速度比前1s的速度大5m/s | |
| D. | 第2s末的速度是第1s末的速度的5倍 |
20.一个蹦极运动的人这样描述它在悬崖上往下跳的感觉:‘这一瞬间大地向我扑来…’.这句话中,大地运动的参考物是( )
| A. | 地球 | B. | 悬崖 | C. | 地面 | D. | 自己 |
17.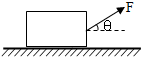 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )| A. | F先减小后增大 | B. | F一直增大 | C. | F的功率变大 | D. | F的功率不变 |
18.一物体做匀变速直线运动,某时刻速度大小为v1=4m/s,1s后的速率大小变为v2=10m/s,在这1s内物体的加速度大小( )
| A. | 可能小于4m/s2 | B. | 不可能等于6m/s2 | C. | 一定等于6 m/s2 | D. | 可能大于l0 m/s2 |