题目内容
质量为M的小物块A静止在离地面高h的水平桌面的边缘,质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰(碰撞时间极短).碰后A离开桌面,其落地点离出发点的水平距离为L.碰后B反向运动.求B后退的距离.已知B与桌面间的动摩擦因数为μ.重力加速度为g.
分析:小物块B与物块A发生正碰的过程,遵守动量守恒定律.碰后A离开桌面做平抛运动,由高度h和水平距离为L求出碰后A的速度,根据动量守恒定律求出B碰后的速度,根据动能定理求解B后退的距离.
解答:解:设t为A从离开桌面至落地经历的时间,V表示刚碰后A的速度,有
h=
gt2
L=Vt
解得 V=L
设v为刚碰后B的速度的大小,由动量守恒定律得,mv0=MV-mv
设B后退的距离为l,由动能定理得
-μmgl=0-
mv2
由以上各式得:l=
答:B后退的距离为
.
h=
| 1 |
| 2 |
L=Vt
解得 V=L
|
设v为刚碰后B的速度的大小,由动量守恒定律得,mv0=MV-mv
设B后退的距离为l,由动能定理得
-μmgl=0-
| 1 |
| 2 |
由以上各式得:l=
(
| ||||||
| 2μg |
答:B后退的距离为
(
| ||||||
| 2μg |
点评:本题是多过程的问题,考查分析物理过程、选择解题规律的能力.对于碰撞过程最基本的规律是动量守恒.对于平抛运动,知道高度和水平距离可以求出平抛运动的初速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在高为h的木箱abcd的水平底板上静置着一个质量为m的小物块A,现用一电动机向上拉木箱,使木箱由静止开始向上运动,且保持电动机的输出功率不变,经时间t木箱达到最大速度,若此时让木箱突然停止运动,小物块由于惯性会继续向上运动,且恰好到达木箱的顶端,空气阻力不计,木箱和小物块的总质量为M,重力加速度为g,求:
如图所示,在高为h的木箱abcd的水平底板上静置着一个质量为m的小物块A,现用一电动机向上拉木箱,使木箱由静止开始向上运动,且保持电动机的输出功率不变,经时间t木箱达到最大速度,若此时让木箱突然停止运动,小物块由于惯性会继续向上运动,且恰好到达木箱的顶端,空气阻力不计,木箱和小物块的总质量为M,重力加速度为g,求: 如图所示,在倾角为θ的固定的足够长斜面上静置一质量为m的小物块A,A与斜面之间的动摩擦因数为μ=tanθ.另有一底面光滑、质量为
如图所示,在倾角为θ的固定的足够长斜面上静置一质量为m的小物块A,A与斜面之间的动摩擦因数为μ=tanθ.另有一底面光滑、质量为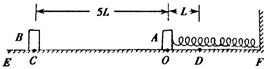 (1)撤去外力后弹簧的最大弹性势能?
(1)撤去外力后弹簧的最大弹性势能?
