��Ŀ����
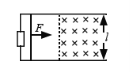
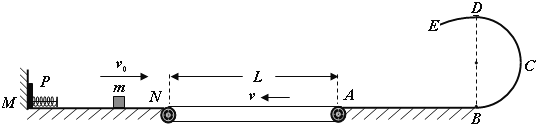
����Ŀ����ͼ��ʾ���⻬ˮƽ������A��B��C������飬�������ֱ�ΪmA=2.0kg��mB=1.0kg��mC=1.0kg������һ�ᵯ�ɽ�A��B��������ӣ�����������ѹ������ʹA��B����鿿�����˹�����������108J�������Դ��ڵ������ڣ���Ȼ��ͬʱ�ͷ�A��B�����ɿ�ʼ�䳤�������ɸպûָ�ԭ��ʱ��Cǡ��4m/s���ٶ�ӭ����B������ײ��ճ����һ����
![]()
��1�����ɸպûָ�ԭ��ʱ��B��C��ײǰ��A��B����ٶȵĴ�С��
��2�������ɵڶ��α�ѹ��ʱ�����ɾ��е����������Ϊ���٣�
���𰸡���1�����ɸպûָ�ԭ��ʱ��B��C��ײǰ��A���ٶ�Ϊ6m/s��B����ٶȴ�С12m/s��
��2�������ɵڶ��α�ѹ��ʱ�����ɾ��е����������Ϊ50J
��������
�����������1�����ɸպûָ�ԭ��ʱ��A��B����ٶȵĴ�С�ֱ�Ϊ��A����B��
�ɶ����غ㶨���У�0=mA��A��mB��B
�˹��̻�е���غ��У�Ep=![]() mA��A2+
mA��A2+![]() mB��B2
mB��B2
����Ep=108J����ã���A=6m/s����B=12m/s��A���ٶ����ң�B���ٶ�����
��2��C��B��ײʱ��C��B��ɵ�ϵͳ�����غ㣬������B��Cճ��ʱ�ٶ�Ϊ�ԡ䣬���У�
mB��B��mC��C=��mB+mC���ԡ䣬�������ݵæԡ�=4m/s���ԡ�ķ�������
�˺�A��B��C��ɵ�ϵͳ�����غ㣬��е���غ㣬�����ɵڶ���ѹ�����ʱ�����ɾ��еĵ������������ΪEp�䣬�Ҵ�ʱA��B��C��������ͬ���ٶȣ���Ϊ�ԣ����У�
�����غ㣺mA��A����mB+mC���ԡ�=��mA+mB+mC���ԣ�
�������ݵæ�=1m/s���Եķ������ң�
��е���غ㣺![]() mA��A2+
mA��A2+![]() ��mB+mC������2=Ep��+
��mB+mC������2=Ep��+![]() ��mA+mB+mC����2��
��mA+mB+mC����2��
�������ݵ�E��p=50J��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�