题目内容
【题目】开普勒1609年一1619年发表了著名的开普勒行星运行三定律,其中第三定律的内容是:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.万有引力定律是科学史上最伟大的定律之一,它于1687年发表在牛顿的《自然哲学的数学原理中》.
(1)请从开普勒行星运动定律等推导万有引力定律(设行星绕太阳的运动可视为匀速圆周运动);
(2)万有引力定律的正确性可以通过“月—地检验”来证明:
如果重力与星体间的引力是同种性质的力,都与距离的二次方成反比关系,那么,由于月心到地心的距离是地球半径的60倍;月球绕地球做近似圆周运动的向心加速度就应该是重力加速度的1/3600.试根据上述思路并通过计算证明:重力和星体间的引力是同一性质的力(已知地球半径为6.4×106m,月球绕地球运动的周期为28天,地球表面的重力加速度为9.8m/s2).
【答案】见解析;
【解析】(1)设行星的质量为m,太阳质量为M,行星绕太阳做匀速圆周运动的轨道半径为R,公转周期为T,太阳对行星的引力为F.
太阳对行星的引力提供行星运动的向心力![]()
根据开普勒第三定律![]() 得
得![]()
故![]()
根据牛顿第三定律,行星和太阳间的引力是相互的,太阳对行星的引力大小与行星的质量成正比,反过来,行星对太阳的引力大小与也与太阳的质量成正比.所以太阳对行星的引力
![]()
写成等式有![]() (G为常量)
(G为常量)
(2)月球绕地球作圆周运动的向心加速度为![]()
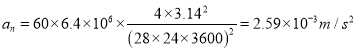
月球做圆周运动的向心加速度与地球表面重力加速度的比为
![]()
所以两种力是同一种性质的力

练习册系列答案
相关题目