题目内容
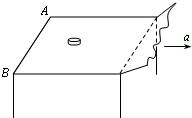
一小圆盘静止在桌布上,位于一方桌的水平桌面的中央.桌布的一边与桌的AB边重合,如图示,已知盘与桌布间的动摩擦因数为μl,盘与桌面间的动摩擦因数为μ2.现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边.若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)

小圆盘在桌布的摩擦力的作用下向前做匀加速直线运动,其加速度为a1,
由牛顿第二定律得μlmg=mal①
故a1=μ1g ②
桌布从突然以恒定加速度a开始抽动至圆盘刚离开桌布这段时间内桌布做匀加速直线运动,设所经历时间为t,桌布通过的位移x,
故x=
at2③
在这段时间内小圆盘移动的距离为x1,
小圆盘通过的位移x1=
a1t2④
小圆盘和桌布之间的相对位移为方桌边长的一半,故有
x=
L+x1⑤
设小圆盘离开桌布时的速度为v1,则有
v12=2alx1⑥
小圆盘离开桌布后在桌面上做匀减速直线运动,
设小圆盘的加速度大小为a2,
则有μ2mg=ma2 ⑦
设小圆盘在桌面上通过的位移大小为x2后便停下,将小圆盘的匀减速运动看做由静止开始的匀加速运动,则有
v12=2a2x2 ⑧
小圆盘没有从桌面上掉下则有
x2+x1≤
L⑨
联立以上各式解得:a≥
μ1g ⑩
即只有桌布抽离桌面的加速度a≥
μ1g时小圆盘才不会从桌面上掉下.
由牛顿第二定律得μlmg=mal①
故a1=μ1g ②
桌布从突然以恒定加速度a开始抽动至圆盘刚离开桌布这段时间内桌布做匀加速直线运动,设所经历时间为t,桌布通过的位移x,
故x=
| 1 |
| 2 |
在这段时间内小圆盘移动的距离为x1,
小圆盘通过的位移x1=
| 1 |
| 2 |
小圆盘和桌布之间的相对位移为方桌边长的一半,故有
x=
| 1 |
| 2 |
设小圆盘离开桌布时的速度为v1,则有
v12=2alx1⑥
小圆盘离开桌布后在桌面上做匀减速直线运动,
设小圆盘的加速度大小为a2,
则有μ2mg=ma2 ⑦
设小圆盘在桌面上通过的位移大小为x2后便停下,将小圆盘的匀减速运动看做由静止开始的匀加速运动,则有
v12=2a2x2 ⑧
小圆盘没有从桌面上掉下则有
x2+x1≤
| 1 |
| 2 |
联立以上各式解得:a≥
| μ1+2μ2 |
| μ2 |
即只有桌布抽离桌面的加速度a≥
| μ1+2μ2 |
| μ2 |

练习册系列答案
相关题目
