Question

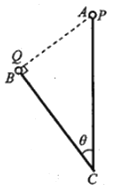
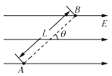
【题目】如图所示，空间有水平向右的匀强电场，A、B是电场中两点，相距L＝20cm，且两点连线与电场线的夹角θ＝37°．现将一质量m＝4.0×10﹣11kg、电荷量q＝﹣1.0×10﹣10C的带电粒子从A点移至B点电场力做功W＝﹣1.6×10﹣9J．粒子重力及空气阻力均不计，sin37°＝0.6，cos37°＝0.8．求：

（1）A、B两点间电势差；

（2）匀强电场的电场强度大小；

（3）若匀强电场的电场强度大小不变，将方向逆时针旋转37°，在A点给该粒子一个沿AB方向的初速度，使其能够到达B点，则此初速度的最小值。

Answer 1

【答案】（1）16V （2）100V/m （3）10m/s

【解析】

（1）根据，即可求解；

（2）由，结合沿着电场强度方向距离，即可求出电场强度；

（3）应用动能定理求出粒子的最小速度。

（1）根据，代入数据，解得：，

（2）由；

代入数据，解得：

（3）电场方向改变后，A、B两点间电势差为，

由于粒子所受电场力方向与初速度方向相反，故到B点的速度为零时，对应的A点初速度为最小值，

由动能定理，则有：；

解得：v0＝10m/s；