��Ŀ����
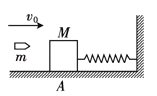
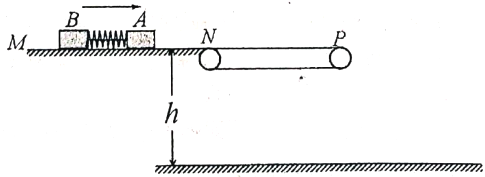
����Ŀ����ͼ��ʾ���㹻���Ĺ⻬ˮƽ̨��M������h=0.80m��ƽ̨�Ҷ˽��ӳ���L=5.4m��ˮƽ���ʹ�NP��A��B������������ֱ�ΪmA=4kg��mB=2kg������֮��ѹ��һ���ᵯ��(����������˨��)����һ��ϸ������������һ����ƽ̨�����ٶ�v=1m/s���������˶���ͻȻ��������ϸ��˲����ѣ��������뵯�����룬֮��A���������˶������ھ�ֹ�Ĵ��ʹ��ϻ�����1.8m����֪����봫�ʹ���Ķ�Ħ��������=0.25��g=10m/s2����
(1)ϸ�߶���˲�䵯���ͷŵĵ�������EP��
(2)���ڻ���A�嵽���ʹ�ʱ���ʹ��������ٶ�v1=1m/s��ʱ�������˶�����A�봫�ʹ�ϵͳ��Ħ������������Q��
(3)���ڻ���A�嵽���ʹ�ʱ���ʹ��������ٶ�v2˳ʱ�������˶��������ۻ���A�˶���P��ʱ��ƽ���˶���ˮƽλ��x��v2�Ĺ�ϵ?(���ʹ����˵����Ӱ뾶�㹻С)
���𰸡�(1)Ep=24J (2)![]() (3)��
(3)��![]() ,
,![]() ;
;![]() ,
,![]() ;
;
��������
(1)��A��B�뵯�ɷ���˲����ٶȷֱ�ΪvA��vB��ȡ����Ϊ�������ɶ����غ㶨�ɵ�:
![]()
A��N�˶��Ĺ��̣����ö��ܶ����ã�![]()
ϸ�߶���˲�䵯���ͷŵĵ�������Ϊ:![]()
��ã�vA=3m/s��vB=��3m/s��Ep=24J
(2)����A��Ƥ�������Ҽ��ٵ�0��������ٵ��봫�ʹ����٣�֮���洫�ʹ������뿪������Ի���ʱ��Ϊ��t
����A���ٶȴ�СΪ:![]()
���˶�ѧ��ʽ��:![]()
![]()
![]()
�����봫�ʹ������Ի���·��Ϊ:![]()
����Ի��������в�����Ħ����:![]()
�����ϸ�ʽ�ã�![]()
(3)��Aƽ�׳��ٶ�Ϊv2��ƽ��ʱ��Ϊt����
![]()
![]()
��t=0.4s
�����ʹ�A˳ʱ���˶����ٶȴﵽijһ�ٽ�ֵvm������A������һֱ���٣�ֱ��ƽ��ʱ���ٶ�ǡΪvm,
��![]()
���vm=6m/s
���ۣ�
��1�������ʹ�˳ʱ���˶����ٶ�![]() ����A�ڴ��ʹ����봫�ʹ���Ի��������봫�ʹ����ֹ�ͬ�ٶȣ�ƽ�׳��ٶȵ���
����A�ڴ��ʹ����봫�ʹ���Ի��������봫�ʹ����ֹ�ͬ�ٶȣ�ƽ�׳��ٶȵ���![]() ��ˮƽ���
��ˮƽ���![]() ��
��
��2�������ʹ�˳ʱ���˶����ٶ�![]() ����A�ڴ��ʹ�������һֱ�����˶���ƽ�׳��ٶȵ���vm=6m/s��ˮƽ���
����A�ڴ��ʹ�������һֱ�����˶���ƽ�׳��ٶȵ���vm=6m/s��ˮƽ���![]() ��
��