题目内容
【题目】某学习小组在实验室发现一盒子内有8个相同的钩码,由于标识模糊,无法知道钩码的质量,为了测定钩码的质量,同学们找到了以下实验器材:一端带定滑轮的长木板,质量为228g的木块,打点计时器,交流电源,纸带,坐标纸,细线等。经商定,他们确定了以下实验方案:

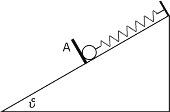
①如图甲所示,将长木板置于水平桌面上,把打点计时器固定在长木板上并与电源连接,纸带穿过打点计时器并与木块相连,细线一端与木块相连,另一端跨过定滑轮挂上钩码,其余钩码都叠放在木块上;
②使木块靠近打点计时器,接通电源,释放木块,打点计时器在纸带上打下一系列点,记下悬挂钩码的个数n;
③将木块上的钩码逐个移到悬挂钩码端,更换纸带,重复实验操作②;
④通过纸带计算出悬挂不同钩码个数所对应的加速度a;
⑤以a为纵坐标,n为横坐标,建立直角坐标系,做出a—n图像。
(1)为了利用以上器材完成实验,还需要哪一项器材____。
A. 秒表
B. 游标卡尺
C.毫米刻度尺
D.垫木
(2)该实验是否必须把木板倾斜,以平衡摩擦?____(选填“是”、“ 否”) 。
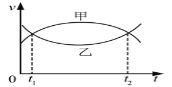
(3)图乙为由实验数据做出的a-n图象,由图可知:
①除了能测定钩码的质量以外,本实验还可测得的物理量是____ (只需填写物理量名称);
②单个钩码的质量为____g(重力加速度取9.8 m/s 2,计算结果保留三位有效数字)。
【答案】C; 否; 木块与桌面间的摩擦因数; 49.6;
【解析】
(1)此实验中必须要用刻度尺对纸带进行测量,则还需要的器材是C;
(2)实验中要对整体进行研究,不需要平衡摩擦力;
(3)对木块与钩码组成的系统,由牛顿第二定律:nmg-μ[(8-n)mg+m木g]=(8m+m木)a,
解得:![]() ,
,
由图象得:n=0时,-μg=a=-4.9,μ=0.5,
由图象的斜率:![]() ,解得m=49.6g;
,解得m=49.6g;
即本实验能测定钩码的质量,还可测得木块与桌面间的摩擦因数;单个钩码的质量为19.6g.

 阅读快车系列答案
阅读快车系列答案