题目内容
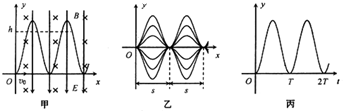
如图甲所示,在x>0的空间中存在沿y轴负方向的匀强电场和垂直于xOy平面向里的匀强磁场,电场强度大小为E,磁感应强度大小为B;一质量为m、带电量为q(q>0)的粒子从坐标原点O处,以初速度v沿x轴正方向射入,粒子的运动轨迹见图甲,不计粒子的重力.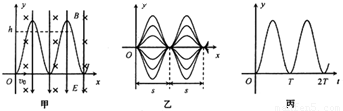
(1)求该粒子运动到y=h时的速度大小v.
(2)现只改变入射粒子初速度的大小,发现初速度大小不同的粒子虽然运动轨迹(y-x曲线)不同,但是,沿x轴方向具有相同的空间周期性,如图乙所示;同时,这些粒子在y轴方向的运动具有相同的时间周期性,即都有相同的周期T=
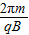 其y-t图象如图丙所示.试求粒子在一个周期T内,沿x轴方向前进的距离s.
其y-t图象如图丙所示.试求粒子在一个周期T内,沿x轴方向前进的距离s.(3)现只改变入射粒子初速度的大小,发现初速度大小不同的粒子虽然运动轨迹(y-x曲线)不同,但是,对任一个轨迹来说,粒子在y=0处和在y方向的最大位移ym处所受的合外力总是大小相等、方向相反.试求当入射粒子的初速度大小为2v时,该粒子在y方向的最大位移ym.
【答案】分析:(1)粒子在运动的过程中只有电场力做功,根据动能定理求出粒子运动到y=h时的速度大小v.
(2)通过图乙可知,所有粒子在一个周期T内沿x轴方向前进的距离相同,即都等于恰好沿x轴方向做匀速直线运动的粒子在T时间内前进的距离s.根据qv1B=qE求出粒子沿x轴方向匀速运动的速度,从而得出一个周期内沿x轴方向运动的位移.
(3)粒子在y=0处和在y方向的最大位移ym处所受的合外力大小相等、方向相反,有q?2v?B-qE=-(qv2B-qE),结合动能定理求出在y方向的最大位移ym
解答:解:(1)由于洛伦兹力不做功,只有电场力做功,由动能定理得:
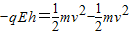 …(1)
…(1)
解得: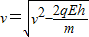 …(2)
…(2)
(2)由图乙可知,所有粒子在一个周期T内沿x轴方向前进的距离相同,即都等于恰好沿x轴方向做匀速直线运动的粒子在T时间内前进的距离s.设粒子恰好沿x轴方向做匀速直线运动的速度大小为v1,则:
qv1B=qE…(3)
又:s=v1T…(4)
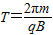 …(5)
…(5)
联立(3)(4)(5)式解得: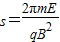 …
…
(3)设粒子在y方向的最大位移为ym,粒子运动的速度大小为v2(方向沿x轴),根据该粒子在y=0处和在y方向的最大位移ym处所受的合外力大小相等、方向相反,可得:
q?2v?B-qE=-(qv2B-qE)…(6)
由动能定理得:
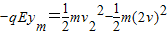 …(7)
…(7)
联立(6)(7)两式解得:
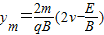 .
.
答:(1)该粒子运动到y=h时的速度大小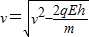 .
.
(2)粒子在一个周期T内,沿x轴方向前进的距离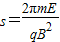 .
.
(3)粒子在y方向的最大位移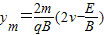 .
.
点评:本题考查了带电粒子在复合场中的运动,过程较复杂,关键理清粒子的运动轨迹,结合动能定理和洛伦兹力和电场力知识进行解决.
(2)通过图乙可知,所有粒子在一个周期T内沿x轴方向前进的距离相同,即都等于恰好沿x轴方向做匀速直线运动的粒子在T时间内前进的距离s.根据qv1B=qE求出粒子沿x轴方向匀速运动的速度,从而得出一个周期内沿x轴方向运动的位移.
(3)粒子在y=0处和在y方向的最大位移ym处所受的合外力大小相等、方向相反,有q?2v?B-qE=-(qv2B-qE),结合动能定理求出在y方向的最大位移ym
解答:解:(1)由于洛伦兹力不做功,只有电场力做功,由动能定理得:
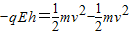 …(1)
…(1)解得:
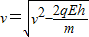 …(2)
…(2)(2)由图乙可知,所有粒子在一个周期T内沿x轴方向前进的距离相同,即都等于恰好沿x轴方向做匀速直线运动的粒子在T时间内前进的距离s.设粒子恰好沿x轴方向做匀速直线运动的速度大小为v1,则:
qv1B=qE…(3)
又:s=v1T…(4)
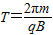 …(5)
…(5)联立(3)(4)(5)式解得:
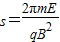 …
…(3)设粒子在y方向的最大位移为ym,粒子运动的速度大小为v2(方向沿x轴),根据该粒子在y=0处和在y方向的最大位移ym处所受的合外力大小相等、方向相反,可得:
q?2v?B-qE=-(qv2B-qE)…(6)
由动能定理得:
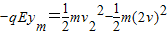 …(7)
…(7)联立(6)(7)两式解得:
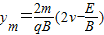 .
.答:(1)该粒子运动到y=h时的速度大小
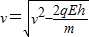 .
.(2)粒子在一个周期T内,沿x轴方向前进的距离
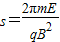 .
.(3)粒子在y方向的最大位移
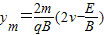 .
.点评:本题考查了带电粒子在复合场中的运动,过程较复杂,关键理清粒子的运动轨迹,结合动能定理和洛伦兹力和电场力知识进行解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

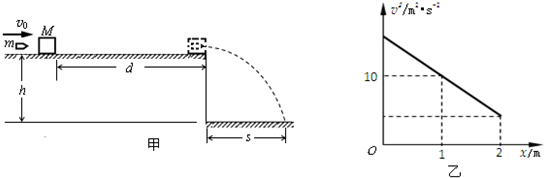 如图甲所示,在高h=0.8m的平台上放置一质量为M=0.99kg的小木块(视为质点),小木块距平台右边缘d=2m,一质量m=0.01kg的子弹沿水平方向射入小木块并留在其中,然后一起向右运动,在平台上运动的v2-x关系如图乙所示.最后,小木块从平台边缘滑出落在距平台右侧水平距离s=0.8m的地面上,g取10m/s2,求:
如图甲所示,在高h=0.8m的平台上放置一质量为M=0.99kg的小木块(视为质点),小木块距平台右边缘d=2m,一质量m=0.01kg的子弹沿水平方向射入小木块并留在其中,然后一起向右运动,在平台上运动的v2-x关系如图乙所示.最后,小木块从平台边缘滑出落在距平台右侧水平距离s=0.8m的地面上,g取10m/s2,求: