��Ŀ����
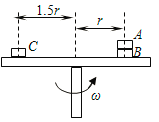
����Ŀ����ͼ��ʾ��ABΪ�������ǰ��һ��ƽֱ��·���䳤��xAB=218m,BCΪˮƽԲ�������Ħ�г���ֱ������ʻ������ٶ�v1=40m/s��Ϊȷ������г���ȫ��Ħ�г��������ǰ������١�����B��������ʱ���ٶ�v2���ܳ���20m/s��Ҫ��Ħ�г��ɾ�ֹ��ʼ����̵�ʱ��������AB���ֱ������֪Ħ�г�����ʱ�����ٶ�a1=4m/s2���ƶ�ʱ�����ٶȴ�СΪa2=8m/s2���Ը�������������Ħ�г���ֱ������ʻ���õ����ʱ����

���𰸡����ʱ��Ϊ11s
��������
�������������Ħ�г��ɾ�ֹ��ʼ���ٵ�����ٶ�v1=40m/s������ʱ�䣺 ![]() ��1����
��1����
���ʱ���ڵ�λ��Ϊ��![]() ��1����
��1����
Ȼ���ټ��ٵ�v2=20m/s������ʱ�䣺![]() ��1����
��1����
��μ��ڵ�λ��Ϊ��![]()
���ʱ��s1+s2=275m��218m��˵��Ħ�г����ܼ��ٵ�40m/s�� ��2����
��Ħ�г����ٵ�����ٶ�Ϊvm������ٽε�λ��Ϊ�� ![]() ��2����
��2����
�����ٵ�v2������λ��Ϊ��![]()
��s1+s2=s
�������� ��ã�vm=36m/s ��2����
����ʱ��Ϊ�� ![]() ������ʱ��Ϊ:
������ʱ��Ϊ: ![]() ��2����
��2����
Ħ�г���ֱ������ʻ���õ����ʱ��Ϊ��t=t1+t2=11s�� ��2����

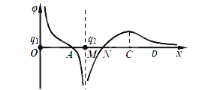
����Ŀ����ͼ��ʾ��t=0ʱ������Ϊ0��2kg����ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ���ȼ���ֱ���˶�������B������ˮƽ�����ȼ���ֱ���˶����辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣬ÿ��2s���������ʱ�������˲ʱ�ٶȼ�¼���±��У��ɴ˿�֪����
t/s | 0 | 2 | 4 | 6 |
v/��ms��1�� | 0 | 8 | 12 | 8 |
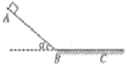
A. �����˶������е�����ٶ�Ϊ12m/s
B. ![]() ��ʱ������ǡ�þ���B��
��ʱ������ǡ�þ���B��
C. t=10s��ʱ������ǡ��ͣ��C��
D. A��B��ľ���С��B��C��ľ���