ЬтФПФкШн
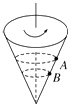
ЁОЬтФПЁПШчЭМЫљЪОЃЌЙтЛЌАыдВаЮЙьЕРДІгкЪњжБЦНУцФкЃЌАыдВаЮЙьЕРгыЙтЛЌЕФЫЎЦНЕиУцЯрЧагкАыдВЕФЖЫЕуA.вЛжЪСПЮЊmЕФаЁЧђдкЫЎЦНЕиУцЩЯCЕуЪмЫЎЦНЯђзѓЕФКуСІFгЩОВжЙПЊЪМдЫЖЏЃЌЕБдЫЖЏЕНAЕуЪБГЗШЅКуСІFЃЌаЁЧђбиЪњжБАыдВаЮЙьЕРдЫЖЏЕНЙьЕРзюИпЕуBЕуЃЌзюКѓгжТфдкЫЎЦНЕиУцЩЯЕФDЕу(ЭМжаЮДЛГі)ЃЎвбжЊAЁЂCМфЕФОрРыЮЊLЃЌжиСІМгЫйЖШЮЊg.
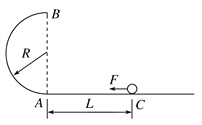
ЃЈ1ЃЉШєЙьЕРАыОЖЮЊRЃЌЧѓаЁЧђЕНДяАыдВаЮЙьЕРBЕуЪБЖдЙьЕРЕФбЙСІFNЃЛ
ЃЈ2ЃЉЮЊЪЙаЁЧђФмдЫЖЏЕНЙьЕРзюИпЕуBЃЌЧѓЙьЕРАыОЖЕФзюДѓжЕRmЃЛ
ЃЈ3ЃЉЙьЕРАыОЖRЖрДѓЪБЃЌаЁЧђдкЫЎЦНЕиУцЩЯЕФТфЕуDЕНAЕуОрРызюДѓЃПзюДѓОрРыxmЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]() ЃЛ
ЃЛ ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЯШгЩЖЏФмЖЈРэЧѓГіаЁЧђЕНДяBЕуЪБЕФЫйЖШДѓаЁЃЌдйгЩХЃЖйЕкЖўЖЈТЩЧѓГіЙьЕРЖдаЁЧђЕФЕЏСІЃЌМДПЩгЩХЃЖйЕкШ§ЖЈТЩЕУЕНаЁЧђЖдЙьЕРЕФбЙСІЃЎЕБаЁЧђЖдЙьЕРЕФбЙСІЧЁКУЮЊСуЪБЃЌЧѓГіЙьЕРАыОЖЕФзюДѓжЕRmЃЛаЁЧђРыПЊBЕуКѓзіЦНХздЫЖЏЃЌИљОнИпЖШЧѓГіЦНХздЫЖЏЕФЪБМфЃЌдйИљОнГѕЫйЖШКЭЪБМфЧѓГіЦНХздЫЖЏЕФЫЎЦНЮЛвЦБэДяЪНЃЌгыЕк1ЬтжааЁЧђОЙ§BЕуЕФЫйЖШСЊСЂЃЌдЫгУЪ§бЇжЊЪЖЧѓНтЃЎ
ЃЈ1ЃЉЩшаЁЧђЕНДядВЙьЕРBЕуЪБЫйЖШЮЊvЃЌДгCЕНBЃЌгЩЖЏФмЖЈРэга![]()
НтЕУЃК ![]()
ОнХЃЖйЕкЖўЖЈТЩгаЃК ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ИљОнХЃЖйЕкШ§ЖЈТЩПЩжЊЃЌаЁЧђЕНДядВЙьЕРBЕуЪБЖдЙьЕРЕФбЙСІЮЊЃК ![]() ЃЌЗНЯђЪњжБЯђЩЯЃЎ
ЃЌЗНЯђЪњжБЯђЩЯЃЎ
ЃЈ2ЃЉЙьЕРАыОЖдНДѓЃЌаЁЧђЕНДязюИпЕуЕФЫйЖШдНаЁЃЌЕБаЁЧђЧЁКУЕНДязюИпЕуЪБЃЌЙьЕРЖдаЁЧђЕФзїгУСІЮЊСуЃЌдђаЁЧђЖдЙьЕРЕФбЙСІвВЮЊСуЃЌДЫЪБЙьЕРАыОЖзюДѓЃЌдђСю![]() ЃЌНтЕУЙьЕРАыОЖЕФзюДѓжЕ
ЃЌНтЕУЙьЕРАыОЖЕФзюДѓжЕ![]()
ЃЈ3ЃЉЩшаЁЧђЦНХздЫЖЏЕФЪБМфЮЊtЃЌдкЪњжБЗНЯђЩЯгаЃК ![]() ЃЌЕУ
ЃЌЕУ![]()
ЫЎЦНЮЛвЦЮЊ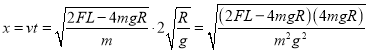
ЕБ![]() ЪБЃЌЫЎЦНЮЛвЦxзюДѓЃЌЕУ
ЪБЃЌЫЎЦНЮЛвЦxзюДѓЃЌЕУ![]()
DЕНAзюДѓОрРыЮЊЃК ![]()

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ