题目内容
10. 长L=0.5m、质量可忽略的杆,其一端连有质量为m=2kg的小球,以另一端O为转轴,它绕O点在竖直平面内做圆周运动,当通过最高点时,如图所示.求:(g取10m/s2)
长L=0.5m、质量可忽略的杆,其一端连有质量为m=2kg的小球,以另一端O为转轴,它绕O点在竖直平面内做圆周运动,当通过最高点时,如图所示.求:(g取10m/s2)(1)当v1=1m/s时,杆对球的作用力大小为多少?是拉力还是支持力?
(2)当v2=4m/s时,杆对球的作用力大小为多少?是拉力还是支持力?
分析 根据牛顿第二定律求出在最高点杆子作用力为零时的速度,从而通过速度的大小判断杆子表现为拉力还是支持力,结合牛顿第二定律求出作用力的大小.
解答 解:(1)小球通过最高点时,当杆子的作用力为零时,有:mg=$m\frac{{v}^{2}}{L}$,
解得v=$\sqrt{gL}=\sqrt{10×0.5}=\sqrt{5}m/s$.
当v1=1m/s时,杆子表现为支持力,根据牛顿第二定律得,mg-F=m$\frac{{{v}_{1}}^{2}}{L}$,
解得F=$mg-m\frac{{{v}_{1}}^{2}}{L}=20-2×\frac{1}{0.5}N=16N$.
(2)v2>v,可知杆子表现为拉力,根据牛顿第二定律得,mg+F′=m$\frac{{{v}_{2}}^{2}}{L}$,
解得$F′=m\frac{{{v}_{2}}^{2}}{L}-mg=2×\frac{16}{0.5}-20$N=44N.
答:(1)当v1=1m/s时,杆对球的作用力大小为16N,杆子对小球表现为支持力.
(2)当v2=4m/s时,杆对球的作用力大小为44N,杆子对小球表现为拉力.
点评 解决本题的关键知道最高点小球做圆周运动向心力的来源,根据牛顿第二定律进行求解,注意在最高点杆子可以表现为拉力,也可以表现为支持力.

练习册系列答案
相关题目
1.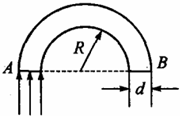 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
 如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )
如图所示,一根粗细均匀的半圆形玻璃棒,折射率为1.5,半径为R,两端面A、B均为正方形,宽度为d.令一束平行光垂直于端面A入射,要使入射光线全都从另一端面B射出,则R与d之比的最小值应为( )| A. | 2 | B. | 1 | C. | 3 | D. | 1.5 |
18.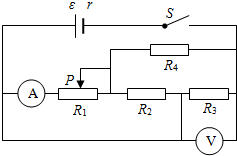 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
 如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
如图所示电路中,电源的内电阻为r、R1、R2、R均为定值电阻,电表均为理想电表.闭合开关S,当滑动变阻器R,的滑动触头P向右滑动时,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )| A. | 电流表示数变大 | B. | 电压表示数变大 | C. | $\frac{△U}{△I}$<r | D. | $\frac{△U}{△I}$>r |
5.有一质量分布均匀的球状行星,设想把一物体放在该行星的中心位置,则此物体与该行星间的万有引力是( )
| A. | 零 | B. | 无穷大 | C. | 无法确定 | D. | 无穷小 |
19.汽车从静止开始保持加速度a作匀加速运动的最长时间为t,此后汽车的运动情况是( )
| A. | 加速为零,速变恒定 | |
| B. | 加速度逐渐减小直到为零,速度逐渐增大直到最大值后保持匀速 | |
| C. | 加速度渐减小直到为零,速度也逐渐减小直至为零 | |
| D. | 加速度逐渐增大到某一值后不变,速度逐渐增大,直到最后匀速 |
20.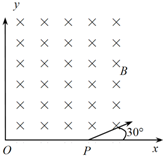 如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy 平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力影响,则下列说法中正确的是( )
如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy 平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力影响,则下列说法中正确的是( )
 如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy 平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力影响,则下列说法中正确的是( )
如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy 平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力影响,则下列说法中正确的是( )| A. | 粒子在磁场中运动所经历的时间可能为$\frac{5πm}{3Bq}$ | |
| B. | 粒子在磁场中运动所经历的时间可能为$\frac{πm}{2Bq}$ | |
| C. | 粒子在磁场中运动所经历的时间可能为$\frac{πm}{Bq}$ | |
| D. | 粒子一定不能通过坐标原点 |
 如图所示,质量为m、电阻为R、ab边长为L的矩形金属单匝线圈竖直放置,水平虚线MN、PQ之间高度差为d,t=0时刻将线圈由图中位置由静止释放,同时在虚线之间加一方向垂直纸面向外的匀强磁场,磁感应强度B大小随时间t的变化关系为B=kt(k为已知常数):t=t1(t1未知)时,ab边进入磁场电流恰好为0;t=t2时ab边穿出磁场前的瞬间线圈加速度为0.(不计空气阻力,重力加速度为g)求:
如图所示,质量为m、电阻为R、ab边长为L的矩形金属单匝线圈竖直放置,水平虚线MN、PQ之间高度差为d,t=0时刻将线圈由图中位置由静止释放,同时在虚线之间加一方向垂直纸面向外的匀强磁场,磁感应强度B大小随时间t的变化关系为B=kt(k为已知常数):t=t1(t1未知)时,ab边进入磁场电流恰好为0;t=t2时ab边穿出磁场前的瞬间线圈加速度为0.(不计空气阻力,重力加速度为g)求: 如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离,设小球A、B与弹簧相互作用过程中无机械能损失,弹簧始终处于弹性限度以内.求当弹簧被压缩到最短时,
如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离,设小球A、B与弹簧相互作用过程中无机械能损失,弹簧始终处于弹性限度以内.求当弹簧被压缩到最短时, 如图所示,左侧的圆形导电环半径r=1.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁感应强度B的变化规律为$\frac{△B}{△t}$=100$\sqrt{2}$•πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原、副线圈匝数之比是多少?
如图所示,左侧的圆形导电环半径r=1.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁感应强度B的变化规律为$\frac{△B}{△t}$=100$\sqrt{2}$•πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原、副线圈匝数之比是多少?