题目内容
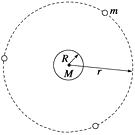
【题目】如图所示，用同种材料制成的一个轨道，AB段为 
圆弧，半径为R，水平放置的BC段长度为R．一小物块质量为m，与轨道间的动摩擦因数为μ，当它从轨道顶端A由静止下滑时，恰好运动到C点静止，那么物块在AB段所受的摩擦力做的功为（ ）
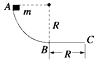
A.μmgR
B.mgR（1－μ）
C.
πμmgR
D. mgR
【答案】B
【解析】物块在AB段所受的摩擦力大小、方向都变化，故不能直接用功的表达式进行计算，可用动能定理进行研究．设在AB段物块克服摩擦力做的功为W，则物块由A到B运用动能定理可得
mgR－W＝ 
－0 ①
物块由B到C运用动能定理可得－μmgR＝0－ ②
①②两式结合，整理可得W＝mgR（1－μ），故B符合题意．
所以答案是：B。
【考点精析】根据题目的已知条件，利用动能定理的综合应用的相关知识可以得到问题的答案，需要掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
练习册系列答案
相关题目
