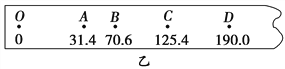题目内容
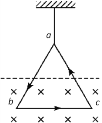
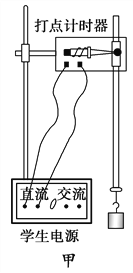
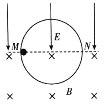
【题目】如图所示,位于竖直平面上的半径为R的圆形光滑绝缘轨道,其上半部分处于竖直向下、场强为E的匀强电场中;下半部分处于水平向里的匀强磁场中。质量为m,带正电荷量为q的小球,从轨道水平直径的M端由静止释放,若小球第一次通过最低点时对轨道的压力为零,求:
(1)磁感应强度B的大小及运动过程中小球对轨道最低点的最大压力;
(2)若要小球在圆形轨道内作完整的圆周运动,小球从轨道水平直径的M端下滑所需的最小速度。
【答案】(1)![]() 竖直向下(2)
竖直向下(2)![]()
【解析】
(1)小球在通过最低点时对轨道的压力为零,由此可知,在最低点时洛伦兹力和重力的合力恰好作为圆周运动的向心力,根据向心力的公式即可以求得磁感应强度B的大小;
当小球反向运动时,小球受到的洛伦兹力的反向反向,在最低点时对小球受力分析,由向心力的公式可以求得小球对轨道最低点的最大压力;
(2)在最高点时,小球的重力和电场力作为圆周运动的向心力的大小,从M点到最高点的过程中,根据动能定理可以求得小球从轨道的水平直径的M端下滑的最小速度。
(1) 设小球向右通过最低点时的速率为v,由题意得:mgR=![]()
qBv-mg=![]()
解得:![]()
小球向左通过最低点时对轨道的压力最大
FN-mg-qBv=![]()
解得:FN=6mg,方向竖直向下;
(2) 要小球完成圆周运动的条件是在最高点满足:
![]()
从M点到最高点由动能定理得:
-mgR-qER=![]()
由以上各式解得:![]() 。
。

练习册系列答案
相关题目