题目内容
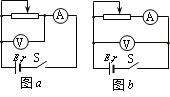
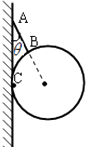
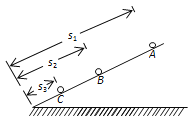
【题目】如图,已知传送带两轮的半径r=1m,传动中传送带不打滑,质量为1kg的物体从光滑轨道A点无初速下滑(A点比B点高h=5m),物体与传送带之间的动摩擦因数μ=0.2,当传送带静止时,物体恰能在C点离开传送带,则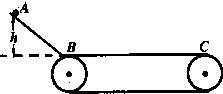
(1)BC两点间距离为多少?
(2)若要使物体从A点无初速释放后能以最短时间到达C点,轮子转动的角速度大小应满足什么条件?
(3)当传送带两轮以12rad/s的角速度顺时针转动时,物体仍从A点无初速释放,在整个过程中物体与皮带系统增加的内能为多少?
【答案】
(1)
解:设物体质量为m,在C点时运动速度为vC,BC间距离为s.
因物体恰在c点离开传送带,则 ![]() ,
,
由动能定理,得 ![]() ,
,
联立得,vC= ![]() m/s,s=22.5m
m/s,s=22.5m
(2)
解:物体以最短时间到达C点,因此BC段物体以最大加速度做匀加速运动,设加速度为a,物体在B、C两点的速度分别为vB、 ![]() ,
,
则a=μg=0.2×10=2m/s2,
![]() ,
,
![]() ,
,
联立解得,v′C=13.8m/s,
轮子转动的角速度 ![]() rad/s
rad/s
(3)
解:物体在BC段加速运动的时间为 ![]() s,
s,
物体与皮带间相对位移为 ![]() m,
m,
Q=fs=f△s=μmg△s=2J
【解析】(1)物体恰能在C点离开,根据牛顿第二定律求出C点的速度,对A到C的过程运用动能定理,求出BC两点间的距离.(2)物体以最短时间到达C点,因此BC段物体以最大加速度做匀加速运动,临界情况是到达C点时,速度恰好与传送带速度相等,根据动能定理求出B点的速度,结合牛顿第二定律和速度位移公式求出到达C点的速度,从而得出轮子转动的角速度大小应满足的条件.(3)根据运动学规律求出相对滑动的路程,结合Q=f△s求出摩擦产生的热量.
【考点精析】解答此题的关键在于理解功能关系的相关知识,掌握当只有重力(或弹簧弹力)做功时,物体的机械能守恒;重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2;合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 (动能定理);除了重力(或弹簧弹力)之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1.

 名校课堂系列答案
名校课堂系列答案