Question

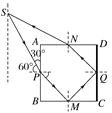
【题目】一立方体透明物体横截面如图所示，底面BC和右侧面CD均镀银(图中粗线)，P、M、Q、N分别为AB边、BC边、CD边、AD边的中点，虚线在ABCD所在的平面内并与AB平行.虚线上有一点光源S，从S发出一条细光线射到P点时与PA的夹角成30°，经折射后直接射到M点，从透明物体的AD面上射出后刚好可以回到S点.试求：(计算中可能会用到 ＝1.41， ＝2.45，sin 15°＝0.26)

（1）透明物体的折射率n；

（2）若光在真空中的速度为c，正方形ABCD的边长为a，则光从S点发出后，经过多长时间射回S点？

Answer 1

【答案】（1）1.225；（2）

【解析】（i）根据题意作光路图，光线在P点发生折射时，入射角为60°，折射角为45°
因此透明物体的折射率

（ii）连接PN，由几何关系可得，PN，PM，QN，QM的长均为a，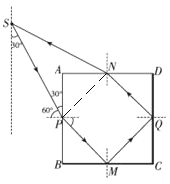

且∠PSN=30°，SN=SP=
光在透明物体中的速度
光透明物体中传播所用的时间 ；
光在透明物体中传播所用的时间
那么光从S点发出射回到S点所经历的总时间为t=t1+t2=