题目内容
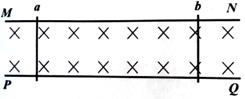
如图所示，相互平行的长直金属导轨MN、PQ位于同一水平面上，导轨间距离为d=1m，处在竖直向下的匀强磁场中，磁感应强度大小为B=0.5T，导轨上与导轨垂直放置质量均为m=0.5kg、电阻均为R=0.8Ω相互平行的导体棒a、b，导体棒与导轨间动摩擦因数均为μ=0.2，重力加速度g=10m/s2，不计导轨及接触处的电阻，认为最大静摩擦等于滑动摩擦力。如果从t-0开始对导体棒a施加平行于导轨的外力F，使a做加速度为a0=3.2m/s2的匀加速运动，导体棒a、b之间距离最够大，a运动中始终未到b处。
（1）求当导体棒a速度多大时，导体棒b会开始运动
（2）在导体棒b开始运动之前，请推导外力F与时间t之间的关系式
（3）若在导体棒b刚要开始运动时撤去外力F，此后导体棒b产生的焦耳热为Q=0.12J,求撤去F后，导体棒a运动的最大距离
【答案】见解析
（1）导体棒b刚开始运动时，电路的电流为I
则 F安 =μmg ………………………①
F安 = BId ………………………②
………………………③
………………………④
解得 
m/s ………………………⑤
（2）对导体棒a，有
………………………⑥
………………………⑦
………………………⑧
………………………⑨
联立解得 F=0.5t+2.6 N…………………⑩
（3）设撤去F后，导体棒a运动的最大距离为s，根据能量守恒有
………………………
解得S=10m ………………………
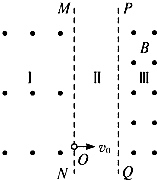如图所示，相互平行的竖直分界面MN、PQ，相距L，将空间分为Ⅰ、Ⅱ、Ⅲ区．Ⅰ、Ⅲ区有水平方向的匀强磁场，Ⅰ区的磁感应强度未知，Ⅲ区的磁感应强度为B；Ⅱ区有竖直方向的匀强电场（图中未画出）．一个质量为m、电荷量为e的电子，自MN上的O点以初速度v0水平射入Ⅱ区，此时Ⅱ区的电场方向竖直向下，以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时，电场突然反向，场强大小不变，这个电子总是经过O点且水平进入Ⅱ区．（不计电子重力）
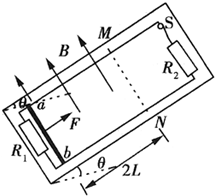如图所示，相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上，相距为L，导轨下端连接一个定值电阻R1，上端通过开关S（S是闭合的）连接一个定值电阻R2．导体棒ab放在导轨上靠近下端的位置，与导轨垂直并接触良好．在导轨平面上虚线MN以下的区域内，存在着垂直穿过斜面向上的匀强磁场．现对导体棒施加平行导轨向上的恒定拉力F，使它沿导轨先向上加速运动，在到达虚线MN之前，导体棒已经开始做匀速运动，速度大小为
