题目内容
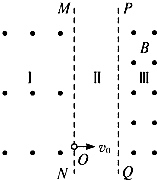 如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)
如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)(1)画出电子运动的轨迹图;
(2)求电子经过界面PQ上两点间的距离;
(3)若Ⅱ区的电场强度大小恒为E,求Ⅰ区的磁感应强度.
分析:(1)电子进入区域Ⅱ后首先做类平抛运动,运动轨迹是一段抛物线;电子进入区域Ⅲ后在洛伦兹力的作用下做匀速圆周运动,轨迹是一段圆弧;再次进入区域Ⅱ后,电子做斜上抛运动,运动轨迹是一段抛物线(和刚进入区域Ⅱ的抛物线是对称的);电子垂直进入区域Ⅰ后,电子做匀速圆周运动,轨迹是一个半圆.
(2)电子在区域Ⅲ中做匀速圆周运动,首先求出运动半径,再由几何关系可求出两点间的距离.
(3)结合第一问和第二问求出电子经过边界MN上的两点间的距离,此为电子在区域Ⅰ中做圆周运动的直径,由洛伦兹力提供向心力公式可求出区域Ⅰ的磁场强度.
(2)电子在区域Ⅲ中做匀速圆周运动,首先求出运动半径,再由几何关系可求出两点间的距离.
(3)结合第一问和第二问求出电子经过边界MN上的两点间的距离,此为电子在区域Ⅰ中做圆周运动的直径,由洛伦兹力提供向心力公式可求出区域Ⅰ的磁场强度.
解答:解:
 (1)电子运动的轨迹如图所示.
(1)电子运动的轨迹如图所示.
(2)电子在Ⅱ区Oa段做类平抛运动,
在a点的速度v1与PQ成θ角,v1sinθ=v0…①
电子在Ⅲ区ab段做匀速圆周运动,洛伦兹力提供向心力,有:
ev1B=
…②
由几何知识有:
=2R1sinθ…③
①②③联立解得:
=
…④
(3)电子在Ⅱ区Oa段运动的竖直位移:
y1=
at2=
?(
)2=
…⑤
电子在bc段做类斜上抛运动,加速度与Oa段等值反向,由运动的对称性得
电子运动的竖直位移:
y2=y1=
…⑥
同样有对称可得电子在c处的速度为:
vc=v0,方向水平向左…⑦
所以,电子在Ⅰ区CO段做匀速圆周运动的半径为:
R′=
(y1+y2+
)…⑧
由牛顿运动定律有:
ev0B=
…⑨
解得:
B′=
(或
)
答:(1)电子运动的轨迹图如图所示.
(2)电子经过界面PQ上两点间的距离为
.
(3)若Ⅱ区的电场强度大小恒为E,Ⅰ区的磁感应强度为
.
 (1)电子运动的轨迹如图所示.
(1)电子运动的轨迹如图所示.(2)电子在Ⅱ区Oa段做类平抛运动,
在a点的速度v1与PQ成θ角,v1sinθ=v0…①
电子在Ⅲ区ab段做匀速圆周运动,洛伦兹力提供向心力,有:
ev1B=
m
| ||
| R1 |
由几何知识有:
. |
| ab |
①②③联立解得:
. |
| ab |
| 2mv0 |
| eB |
(3)电子在Ⅱ区Oa段运动的竖直位移:
y1=
| 1 |
| 2 |
| eE |
| 2m |
| L |
| v0 |
| eEL2 | ||
2m
|
电子在bc段做类斜上抛运动,加速度与Oa段等值反向,由运动的对称性得
电子运动的竖直位移:
y2=y1=
| eEL2 | ||
2m
|
同样有对称可得电子在c处的速度为:
vc=v0,方向水平向左…⑦
所以,电子在Ⅰ区CO段做匀速圆周运动的半径为:
R′=
| 1 |
| 2 |
. |
| ab |
由牛顿运动定律有:
ev0B=
m
| ||
| R′ |
解得:
B′=
| mv0 | ||||||
|
2m2
| ||
2m2
|
答:(1)电子运动的轨迹图如图所示.
(2)电子经过界面PQ上两点间的距离为
| 2mv0 |
| eB |
(3)若Ⅱ区的电场强度大小恒为E,Ⅰ区的磁感应强度为
| mv0 | ||||||
|
点评:该题考察了电子在电场中的偏转和在磁场中的匀速圆周运动,此题要求首先要分析电子在各个区域内的运动情况,画出电子的运动轨迹图,了解图中的几何关系.利用电子在电场中偏转时的速度的合成与分解,解决电子在电场中运动的相关问题;利用电子在匀速圆周运动的半径和周期公式,结合洛伦兹力提供向心力可解答电子在磁场中运动的相关问题.
电子从磁场边界以一定的角度射入只有一个边界的匀强磁场,当再次射出磁场时,速度与边界的夹角与原来的相等.解题时充分利用这个结论,对解题有非常大的帮助.
电子从磁场边界以一定的角度射入只有一个边界的匀强磁场,当再次射出磁场时,速度与边界的夹角与原来的相等.解题时充分利用这个结论,对解题有非常大的帮助.

练习册系列答案
相关题目
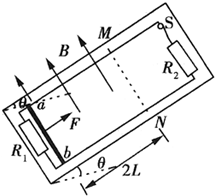 如图所示,相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上,相距为L,导轨下端连接一个定值电阻R1,上端通过开关S(S是闭合的)连接一个定值电阻R2.导体棒ab放在导轨上靠近下端的位置,与导轨垂直并接触良好.在导轨平面上虚线MN以下的区域内,存在着垂直穿过斜面向上的匀强磁场.现对导体棒施加平行导轨向上的恒定拉力F,使它沿导轨先向上加速运动,在到达虚线MN之前,导体棒已经开始做匀速运动,速度大小为
如图所示,相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上,相距为L,导轨下端连接一个定值电阻R1,上端通过开关S(S是闭合的)连接一个定值电阻R2.导体棒ab放在导轨上靠近下端的位置,与导轨垂直并接触良好.在导轨平面上虚线MN以下的区域内,存在着垂直穿过斜面向上的匀强磁场.现对导体棒施加平行导轨向上的恒定拉力F,使它沿导轨先向上加速运动,在到达虚线MN之前,导体棒已经开始做匀速运动,速度大小为
