题目内容
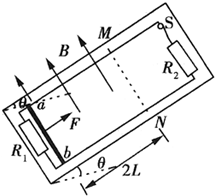 如图所示,相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上,相距为L,导轨下端连接一个定值电阻R1,上端通过开关S(S是闭合的)连接一个定值电阻R2.导体棒ab放在导轨上靠近下端的位置,与导轨垂直并接触良好.在导轨平面上虚线MN以下的区域内,存在着垂直穿过斜面向上的匀强磁场.现对导体棒施加平行导轨向上的恒定拉力F,使它沿导轨先向上加速运动,在到达虚线MN之前,导体棒已经开始做匀速运动,速度大小为v=
如图所示,相互平行的光滑金属导轨固定在倾角为θ=30°的绝缘斜面上,相距为L,导轨下端连接一个定值电阻R1,上端通过开关S(S是闭合的)连接一个定值电阻R2.导体棒ab放在导轨上靠近下端的位置,与导轨垂直并接触良好.在导轨平面上虚线MN以下的区域内,存在着垂直穿过斜面向上的匀强磁场.现对导体棒施加平行导轨向上的恒定拉力F,使它沿导轨先向上加速运动,在到达虚线MN之前,导体棒已经开始做匀速运动,速度大小为v=| Lg |
| R |
| 2 |
(1)磁感应强度B和拉力F的大小;
(2)导体棒从ab开始运动到回到初始位置ab的过程中电阻R1产生的热量Q1;
(3)若在导体棒ab再次进入磁场时没有断开开关S,则导体棒ab将如何运动.
分析:(1)由题,ab棒在到达MN之前已经做匀速运动,受力平衡,由平衡条件可得到拉力F与重力、安培力的关系式,并由法拉第定律、欧姆定律推导出安培力与速度的关系;当导体棒到达MN时,立即撤去拉力F,导体棒先向上做匀减速运动,后向下做匀加速运动,两个过程加速度相同,两个过程具有对称性,棒滑回MN时的速度大小相等.由题,导体棒进入磁场后又恰好做匀速运动,再用同样的方法得到拉力F与重力、安培力的关系式,联立几个关系式,即可求得B和F.
(2)根据能量守恒列式,分别对ab棒在磁场中上滑和下滑时回路产生的热量,再根据串并联关系求解电阻R1产生的热量Q1;
(3)若在导体棒ab再次进入磁场时没有断开开关S,分析安培力与重力沿斜面向下的分力关系,判断其运动情况.
(2)根据能量守恒列式,分别对ab棒在磁场中上滑和下滑时回路产生的热量,再根据串并联关系求解电阻R1产生的热量Q1;
(3)若在导体棒ab再次进入磁场时没有断开开关S,分析安培力与重力沿斜面向下的分力关系,判断其运动情况.
解答:解:(1)棒ab到达MN前已经开始做匀速运动,受力平衡,则有
F=mgsinθ+FA1,
而又有FA1=BI1L,I1=
=
=
,
得FA1=
联立以上各式得 F=mgsinθ+
①
ab棒滑回到MN时,速度大小仍为v,也做匀速运动,则有
mgsinθ=FA2,
又FA2=BI2L,I2=
,
得FA2=
由上面两式得:mgsinθ=
②
由题,v=
联立①②③解得,B=
=
,F=2.5mgsinθ=1.25mg.
(2)根据能量守恒得
ab棒上滑过程:F?2L=QR1+QR2+Qr+mgsinθ?2L+
mv2
而QR1=QR2,Qr=QR1+QR2,
解得:QR1=
(3mgsinθL-
mgL)=
mgL
ab棒下滑过程:mgsinθ?2L=QR1′+Qr′
又QR1′=2Qr′
解得,QR1′=
mgLsinθ=
mgL
故整个过程中,电阻R1产生的热量Q1=QR1+QR1′=
mgL
(3)若在导体棒ab再次进入磁场时没有断开开关S,ab棒再次进入磁场时,所受的安培力大小等于FA1,
由上知道,FA1>FA2,mgsinθ=FA2,
故有mgsinθ<FA1,则知ab棒再次进入磁场时所受安培力大于重力沿斜面向下的分力,则ab棒将做减速运动,安培力减小,加速度减小,即导体棒ab做加速度减小的减速运动.
答:
(1)磁感应强度为
,拉力F的大小为1.25mg;
(2)导体棒从ab开始运动到回到初始位置ab的过程中电阻R1产生的热量Q1为
mgL.
(3)若在导体棒ab再次进入磁场时没有断开开关S,则导体棒ab做加速度减小的减速运动.
F=mgsinθ+FA1,
而又有FA1=BI1L,I1=
| BLv | ||
|
| BLv | ||||
|
| BLv |
| R |
得FA1=
| B2L2v |
| R |
联立以上各式得 F=mgsinθ+
| B2L2v |
| R |
ab棒滑回到MN时,速度大小仍为v,也做匀速运动,则有
mgsinθ=FA2,
又FA2=BI2L,I2=
| BLv | ||
R+
|
得FA2=
| 2B2L2v |
| 3R |
由上面两式得:mgsinθ=
| 2B2L2v |
| 3R |
由题,v=
| Lg |
联立①②③解得,B=
| 3mgRsinθ | ||
2L2
|
| 3mgR | ||
4L2
|
(2)根据能量守恒得
ab棒上滑过程:F?2L=QR1+QR2+Qr+mgsinθ?2L+
| 1 |
| 2 |
而QR1=QR2,Qr=QR1+QR2,
解得:QR1=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
ab棒下滑过程:mgsinθ?2L=QR1′+Qr′
又QR1′=2Qr′
解得,QR1′=
| 4 |
| 3 |
| 2 |
| 3 |
故整个过程中,电阻R1产生的热量Q1=QR1+QR1′=
| 11 |
| 12 |
(3)若在导体棒ab再次进入磁场时没有断开开关S,ab棒再次进入磁场时,所受的安培力大小等于FA1,
由上知道,FA1>FA2,mgsinθ=FA2,
故有mgsinθ<FA1,则知ab棒再次进入磁场时所受安培力大于重力沿斜面向下的分力,则ab棒将做减速运动,安培力减小,加速度减小,即导体棒ab做加速度减小的减速运动.
答:
(1)磁感应强度为
| 3mgR | ||
4L2
|
(2)导体棒从ab开始运动到回到初始位置ab的过程中电阻R1产生的热量Q1为
| 11 |
| 12 |
(3)若在导体棒ab再次进入磁场时没有断开开关S,则导体棒ab做加速度减小的减速运动.
点评:本题关键是通过分析棒ab的受力情况来分析其运动情况,安培力的计算是关键,还要抓住对称性,分析得出ab棒返回时MN时的速度与上滑时速度大小相等.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
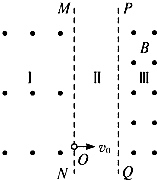 如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)
如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)
