题目内容
9.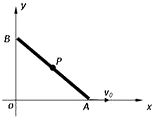 在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )
在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点A、B分别被约束在x轴和y轴上,现让杆的A端沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,某一时刻杆AB与x轴的夹角为θ.关于P点的运动轨迹和P点的运动速度大小v的表达式,下列说法中正确的是( )| A. | P点的运动轨迹是抛物线的一部分 | B. | P点的运动轨迹是圆弧的一部分 | ||
| C. | P点的速度大小为v=v0tanθ | D. | P点的速度大小为$\frac{{v}_{0}}{2sinθ}$ |
分析 设P点坐标为(x,y),则A、B点的坐标分别为(0,2x)、(0,2y),AB长度一定,设为L,列式求解出x与y的关系式,即为P点的轨迹方程;P点的轨迹是圆,速度是切线方向,画出轨迹图,结合几何关系得到P点速度方向与杆的方向的夹角,P点的速度沿着杆方向的分速度与A点速度沿着杆方向的分速度相等.
解答 解:A、B、设P点坐标为(x,y),则A、B点的坐标分别为(2x,0)、(0,2y),AB长度一定,设为L,根据勾股定理,有:
(2x)2+(2y)2=L2
解得:
x2+y2=($\frac{L}{2}$)2
故P点的运动轨迹是圆弧,半径为$\frac{L}{2}$;故A错误,B正确;
C、D、画出运动轨迹,如图: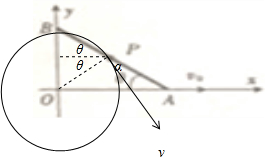
速度v与杆的夹角α=90°-2θ;
由于杆子不可以伸长,故P点的速度沿着杆方向的分速度与A点速度沿着杆方向的分速度相等,故:
vcosα=v0cosθ
vcos(90°-2θ)=v0cosθ
解得:
v=$\frac{{v}_{0}}{2sinθ}$,故C错误,D正确;
故选:BD.
点评 本题关键是采用运动的合成与分解的方法进行研究,找出点P的运动方向是关键,同时掌握圆的方程.

练习册系列答案
相关题目
19.下述对半导体、超导体的应用说法正确的是( )
| A. | 利用光敏电阻制成的自动开关,可使照明灯在天亮时关,在天暗时开 | |
| B. | 在有些电冰箱中,使用了热敏电阻 | |
| C. | 半导体材料的电阻随温度的增加而增加 | |
| D. | 若采用超导电缆输电,就不需要高压输电 |
17.如图是某电源的路端电压与电流的关系图象,下列结论正确的是( )
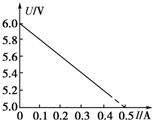

| A. | 电源的电动势为6.0 V | B. | 电源的内阻为12Ω | ||
| C. | 电流为0.2 A时的外电阻是28Ω | D. | 电源的短路电流为0.5 A |
4.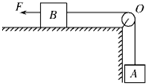 如图所示,重力为G1=10N的物体A与重力为G2=50N的物体B用跨过定滑轮的轻绳连接,B物体放在水平桌面上,且绳的BO段水平,AO段竖直,已知B与桌面间的最大静摩擦力Fm=8N,为使A、B均保持静止,可对B物体加一个水平向左的拉力F,则F的值可能为( )
如图所示,重力为G1=10N的物体A与重力为G2=50N的物体B用跨过定滑轮的轻绳连接,B物体放在水平桌面上,且绳的BO段水平,AO段竖直,已知B与桌面间的最大静摩擦力Fm=8N,为使A、B均保持静止,可对B物体加一个水平向左的拉力F,则F的值可能为( )
 如图所示,重力为G1=10N的物体A与重力为G2=50N的物体B用跨过定滑轮的轻绳连接,B物体放在水平桌面上,且绳的BO段水平,AO段竖直,已知B与桌面间的最大静摩擦力Fm=8N,为使A、B均保持静止,可对B物体加一个水平向左的拉力F,则F的值可能为( )
如图所示,重力为G1=10N的物体A与重力为G2=50N的物体B用跨过定滑轮的轻绳连接,B物体放在水平桌面上,且绳的BO段水平,AO段竖直,已知B与桌面间的最大静摩擦力Fm=8N,为使A、B均保持静止,可对B物体加一个水平向左的拉力F,则F的值可能为( )| A. | 3N | B. | 10N | C. | 15N | D. | 20N |
14.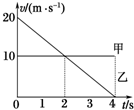 甲、乙两车同时、同地、向同一个方向做直线运动,它们在0~4s内运动的v-t图象如图所示,由图象可知( )
甲、乙两车同时、同地、向同一个方向做直线运动,它们在0~4s内运动的v-t图象如图所示,由图象可知( )
 甲、乙两车同时、同地、向同一个方向做直线运动,它们在0~4s内运动的v-t图象如图所示,由图象可知( )
甲、乙两车同时、同地、向同一个方向做直线运动,它们在0~4s内运动的v-t图象如图所示,由图象可知( )| A. | 在第2s末,两车处于同一位置 | |
| B. | 在第3s末,两车处于同一位置 | |
| C. | 在0~4s内,甲的加速度和乙的加速度的大小相等 | |
| D. | 在0~4s内,甲、乙两车的平均速度相等 |
1.一根导线两端加上电压U,导体中自由电子定向移动的平均速率为v,现将导线均匀拉长至横截面半径为原来的$\frac{1}{2}$,然后两端加上电压U,则导线中自由电子定向移动的平均速率为( )
| A. | $\frac{v}{2}$ | B. | $\frac{\sqrt{2}v}{2}$ | C. | $\frac{v}{4}$ | D. | $\frac{\sqrt{2}v}{4}$ |
10.有一只电压表内阻是100Ω,量程为0.2V,现要将它改装成量程为2V的电压表,则应在原电压表上( )
| A. | 并联900Ω的电阻 | B. | 并联0.1Ω的电阻 | C. | 串联900Ω的电阻 | D. | 串联0.1Ω的电阻 |