题目内容
2. 如图所示,A、B、C三物块均为m,置于光滑水平面上,A、B间夹有已完全压紧不能再压缩的弹簧.两物块用细绳相连,使弹簧不能伸展,物块C以初速度v0沿AB直线方向向A运动,相碰后A与C粘合在一起,然后连接A、B的细绳因受到扰动而突然断开,弹簧伸长,从而使B与A、C分离,脱离弹簧后B的速度为v0,求:
如图所示,A、B、C三物块均为m,置于光滑水平面上,A、B间夹有已完全压紧不能再压缩的弹簧.两物块用细绳相连,使弹簧不能伸展,物块C以初速度v0沿AB直线方向向A运动,相碰后A与C粘合在一起,然后连接A、B的细绳因受到扰动而突然断开,弹簧伸长,从而使B与A、C分离,脱离弹簧后B的速度为v0,求:(1)碰撞瞬后间A、B速度大小?
(2)弹簧释放的弹性势能大小.
分析 (1)C与A、B碰撞过程中动量守恒,由动量守恒定律可以求出碰后瞬间三者的共同速度;
(2)细绳断开后,AC与B分离过程中系统的动量守恒,由动量守恒定律可以列方程;在弹簧弹开过程中,系统的机械能守恒,由机械能守恒定律可以列方程,解方程即可求出弹簧释放的弹性势能.
解答 解:(1)取水平向右为正方向,设碰后三个物体的共同速度为v,由动量守恒定律得:
mv0=3mv…①
得:v=$\frac{1}{3}{v}_{0}$
(2)设B离开弹簧时,AC的速度大小为v1,由动量守恒定律得:
3mv=2mv1+mv0…②
设弹簧释放的弹性势能为Ep,从细绳断开到B与弹簧分开的过程中系统的机械能守恒,则有:
$\frac{1}{2}$(3m)v2+Ep=$\frac{1}{2}$(2m)${v}_{1}^{2}$+$\frac{1}{2}m{v}_{0}^{2}$…③
由①②③式得弹簧所释放的势能为:Ep=$\frac{1}{3}m{v}_{0}^{2}$…④
答:(1)碰撞瞬后间A、B速度大小为$\frac{1}{3}{v}_{0}$.
(2)弹簧释放的弹性势能大小为$\frac{1}{3}$mv02.
点评 本题要注意分析清楚物体运动过程,明确碰撞过程和弹簧释放过程的基本规律:动量守恒定律、能量守恒定律,并能分过程列式.

练习册系列答案
相关题目
12.下列说法中正确的是( )
| A. | 物体有加速度,速度就增大 | |
| B. | 速度改变量△v越大,加速度就越大 | |
| C. | 加速度增大,速度一定增大 | |
| D. | 速度很大的物体,其加速度可以很小 |
13. 中国空军八一飞行表演队在训练中,6架表演机保持队形,直刺苍穹,做出了多个高难度动作,如图所示,下列关于飞机运动情况的说法正确的是( )
中国空军八一飞行表演队在训练中,6架表演机保持队形,直刺苍穹,做出了多个高难度动作,如图所示,下列关于飞机运动情况的说法正确的是( )
 中国空军八一飞行表演队在训练中,6架表演机保持队形,直刺苍穹,做出了多个高难度动作,如图所示,下列关于飞机运动情况的说法正确的是( )
中国空军八一飞行表演队在训练中,6架表演机保持队形,直刺苍穹,做出了多个高难度动作,如图所示,下列关于飞机运动情况的说法正确的是( )| A. | 地面上的人看到飞机飞过,是以地面为参考系 | |
| B. | 飞行员看到观礼台向后掠过,是以飞机为参考系 | |
| C. | 以编队中某一飞机为参考系,其他飞机是静止的 | |
| D. | 以编队中某一飞机为参考系,其他飞机是运动的 |
10. 2010年10月1日我国成功发射了“嫦娥二号”探月卫星,如图所示是火箭点火升空瞬间的照片,关于这一瞬间的火箭的速度和加速度的判断,下列说法正确的是( )
2010年10月1日我国成功发射了“嫦娥二号”探月卫星,如图所示是火箭点火升空瞬间的照片,关于这一瞬间的火箭的速度和加速度的判断,下列说法正确的是( )
 2010年10月1日我国成功发射了“嫦娥二号”探月卫星,如图所示是火箭点火升空瞬间的照片,关于这一瞬间的火箭的速度和加速度的判断,下列说法正确的是( )
2010年10月1日我国成功发射了“嫦娥二号”探月卫星,如图所示是火箭点火升空瞬间的照片,关于这一瞬间的火箭的速度和加速度的判断,下列说法正确的是( )| A. | 火箭的速度很小,但加速度可能较大 | |
| B. | 火箭的速度很大,加速度也很大 | |
| C. | 火箭的速度很小,所以加速度也很小 | |
| D. | 火箭的速度很大,但加速度一定很小 |
5. 利用一理想变压器给一灯泡供电,输入电压不变,当开关S由c扳到b时,副线圈匝数变少,则( )
利用一理想变压器给一灯泡供电,输入电压不变,当开关S由c扳到b时,副线圈匝数变少,则( )
 利用一理想变压器给一灯泡供电,输入电压不变,当开关S由c扳到b时,副线圈匝数变少,则( )
利用一理想变压器给一灯泡供电,输入电压不变,当开关S由c扳到b时,副线圈匝数变少,则( )| A. | 原线圈的电流减小 | B. | 电灯亮度变亮 | ||
| C. | 灯泡两端的电压变小 | D. | 输入变压器的电功率不变 |
2.如图(a)左侧的调压装置可视为理想变压器,负载电路中 R=55Ω, 、
、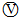 为理想电流表和电压表.若原线圈接入如图(b)所示的正弦交变电压,电压表的示数为 110V,下列表述正确的是( )
为理想电流表和电压表.若原线圈接入如图(b)所示的正弦交变电压,电压表的示数为 110V,下列表述正确的是( )
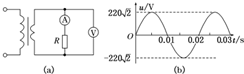
 、
、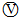 为理想电流表和电压表.若原线圈接入如图(b)所示的正弦交变电压,电压表的示数为 110V,下列表述正确的是( )
为理想电流表和电压表.若原线圈接入如图(b)所示的正弦交变电压,电压表的示数为 110V,下列表述正确的是( ) 
| A. | 电流表的示数为 2 A | |
| B. | 原、副线圈匝数比为 1:2 | |
| C. | 电压表的示数为电压的有效值 | |
| D. | 原线圈中交变电压的频率为 100 Hz |
3.如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,闭合开关s后,当滑动变阻器触片P向下移动时,则( )


| A. | 电流表示数增大 | |
| B. | 电压表示数减小 | |
| C. | 电源的总功率增大 | |
| D. | 电阻R1上消耗的电功率大于电阻R2上消耗的电功率 |
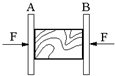 如图所示,在两块相同的竖直木板A、B之间夹着一块重力为30N的长方体物体.用两个大小均为F=100N的水平力压物体,物体与木板之间的动摩擦因数均为μ=0.2.求:
如图所示,在两块相同的竖直木板A、B之间夹着一块重力为30N的长方体物体.用两个大小均为F=100N的水平力压物体,物体与木板之间的动摩擦因数均为μ=0.2.求: