题目内容
A B两个质点沿直线同时从甲处向乙处运动,A以vA=3m/s的速度做匀速运动,B作初速度为零,加速度aB=3m/s2的匀加速运动,当 B 与A在途中相遇时,即改做加速度aB=-2m/s2匀减速运动,求,AB质点何时相距最远?
分析:开始过程,B追赶A,当两者速度相等时相距最远,当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,比较这两次的数值,便可得到答案
解答:解:开始的一段时间内,B追赶A,当两者速度相等时相距最远,设所需时间为t1,则:vA=aBt1
所以,t1=
=
s=1s
两者距离为:s=vAt1-
=3×1-
×3×12m=1.5m
设经过总时间t,两者第一次相遇,则有:vAt=
aBt2
解得:t=2s
此时B速度为:vB=aBt=3×2m/s=6m/s
当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,设从相遇到速度再次相等用时t2,则:t2=
=
s=1.5s
此时两者相距:s′=vBt2-
aB
-vAt2=6×1.5-0.5×2×1.52-3×1.5m=2.25m
由于s′>s
从出发所需时间:T=t+t1=3.5s
答:当t=3.5s时,相距最远距离为2.25m
所以,t1=
| vA |
| aB |
| 3 |
| 3 |
两者距离为:s=vAt1-
| 1 |
| 2 |
| aBt | 2 1 |
| 1 |
| 2 |
设经过总时间t,两者第一次相遇,则有:vAt=
| 1 |
| 2 |
解得:t=2s
此时B速度为:vB=aBt=3×2m/s=6m/s
当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,设从相遇到速度再次相等用时t2,则:t2=
| vB-vA |
| aB′ |
| 6-3 |
| 2 |
此时两者相距:s′=vBt2-
| 1 |
| 2 |
| ′t | 2 2 |
由于s′>s
从出发所需时间:T=t+t1=3.5s
答:当t=3.5s时,相距最远距离为2.25m
点评:解决本题的关键知道两者速度相等时,两者相距最远,两者位移之差就是相距的位移

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
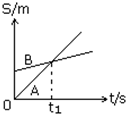 如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是( )
如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是( )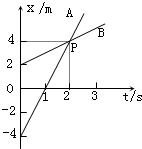 A、B两个质点沿一直线运动的位移-时间图象如图示,由图可知( )
A、B两个质点沿一直线运动的位移-时间图象如图示,由图可知( )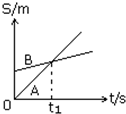 如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是
如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是