题目内容
A B两个质点沿直线同时从甲处向乙处运动,A以vA=3m/s的速度做匀速运动,B作初速度为零,加速度aB=3m/s2的匀加速运动,当 B 与A在途中相遇时,即改做加速度aB=-2m/s2匀减速运动,求,AB质点何时相距最远?
解:开始的一段时间内,B追赶A,当两者速度相等时相距最远,设所需时间为t1,则:vA=aBt1
所以,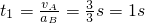
两者距离为:s=
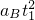 =3×
=3×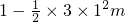 =1.5m
=1.5m
设经过总时间t,两者第一次相遇,则有:

解得:t=2s
此时B速度为:vB=aBt=3×2m/s=6m/s
当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,设从相遇到速度再次相等用时t2,则: =
= s=1.5s
s=1.5s
此时两者相距:s′=
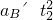 -vAt2=6×1.5-0.5×2×1.52-3×1.5m=2.25m
-vAt2=6×1.5-0.5×2×1.52-3×1.5m=2.25m
由于s′>s
从出发所需时间:T=t+t1=3.5s
答:当t=3.5s时,相距最远距离为2.25m
分析:开始过程,B追赶A,当两者速度相等时相距最远,当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,比较这两次的数值,便可得到答案
点评:解决本题的关键知道两者速度相等时,两者相距最远,两者位移之差就是相距的位移
所以,
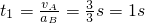
两者距离为:s=

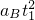 =3×
=3×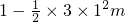 =1.5m
=1.5m设经过总时间t,两者第一次相遇,则有:


解得:t=2s
此时B速度为:vB=aBt=3×2m/s=6m/s
当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,设从相遇到速度再次相等用时t2,则:
 =
= s=1.5s
s=1.5s此时两者相距:s′=

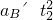 -vAt2=6×1.5-0.5×2×1.52-3×1.5m=2.25m
-vAt2=6×1.5-0.5×2×1.52-3×1.5m=2.25m由于s′>s
从出发所需时间:T=t+t1=3.5s
答:当t=3.5s时,相距最远距离为2.25m
分析:开始过程,B追赶A,当两者速度相等时相距最远,当两者第一次相遇后,改为A追赶B,当两者速度相等时,再次相距最远,比较这两次的数值,便可得到答案
点评:解决本题的关键知道两者速度相等时,两者相距最远,两者位移之差就是相距的位移

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
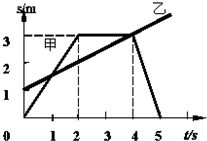 如图是甲、乙二个质点沿同一直线运动的s-t图象,根据图象判断,则下列说法正确的是( )
如图是甲、乙二个质点沿同一直线运动的s-t图象,根据图象判断,则下列说法正确的是( )| A、0~2s内甲的速度先比乙小后比乙大,在1S末甲追上乙 | B、2s~4s内甲做匀速乙做加速运动在4S末乙追上甲 | C、0~4s内甲、乙两质点间的距离是先减小后增加再减小 | D、第5秒内乙的速度大于甲的速度 |
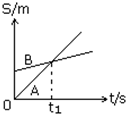 如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是( )
如图所示,A、B两个质点沿直线运动的位移-时间图象,以下说法正确的是( )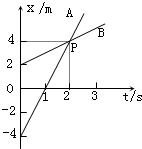 A、B两个质点沿一直线运动的位移-时间图象如图示,由图可知( )
A、B两个质点沿一直线运动的位移-时间图象如图示,由图可知( )