题目内容
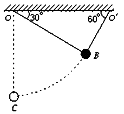
【题目】如图所示,质量为0.5千克的物体,从球面顶点,沿半径R=1米的粗糙半球面由静止下滑,物体落地时速度大小为3米/秒,空气阻不计,求: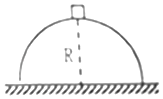
(1)物体克服摩擦力所做的功;
(2)物体离开球面时下降的高度.
【答案】
(1)解:物体下滑过程受重力、支持力、摩擦力作用,支持力不做功,故对下滑过程应用动能定理可得: ![]() ,
,
所以, ![]() ;
;
所以,物体克服摩擦力所做的功为2.75J;
答:物体克服摩擦力所做的功为2.75J;
(2)解:设物体离开球面时下降的高度为h,那么由动能定理可得: ![]() ;
;
物体在刚要离开球面时,球面对物体的支持力为零,即重力沿径向分量正好等于向心力,即 ![]() ;
;
所以,mg(R﹣h)=2(mgh+Wf),
所以, ![]() ;
;
答:物体离开球面时下降的高度为0.7m.
【解析】(1)根据物体从静止下滑到物体落地整个过程应用动能定理求解;(2)根据物体离开球面时球面对物体的支持力为零,再对物体开始运动到离开球面过程应用动能定理即可求解.
【考点精析】根据题目的已知条件,利用向心力和变力做功的相关知识可以得到问题的答案,需要掌握向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力;利用动能定理计算力的功,特别是变力所做的功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目