题目内容
【题目】如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2 , 空气阻力忽略不计.求: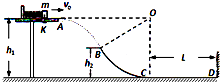
(1)小物块由A到B的运动时间t;
(2)解除锁定前弹簧所储存的弹性势能Ep;
(3)小物块与轨道CD间的动摩擦因数μ.
【答案】
(1)解:小物块由A运动到B的过程中做平抛运动,在竖直方向上根据自由落体运动规律可知:
h1﹣h2= ![]() gt2
gt2
小物块由A运动到B的时间为:t= ![]() =
= ![]() s≈0.346s
s≈0.346s
答:小物块由A到B的运动时间为0.346s
(2)解:根据图中几何关系可知:h2=h1(1﹣cos∠BOC),
代入数据解得:∠BOC=60°
设小滑块从A点离开时速度大小为v,根据平抛运动规律有:
tan60°= ![]() ,
,
代入数据解得:v=2m/s
根据功能关系可知,原来压缩的弹簧储存的弹性势能为t2:
Ep= ![]() mv2=2J
mv2=2J
答:解除锁定前弹簧所储存的弹性势能为2J;
(3)解:依据题意根据功能关系有:
mgh1+EP=μmgL
代入数据解得:μ= ![]() .
.
答:小物块与轨道CD间的动摩擦因数为 ![]()
【解析】(1)首先要清楚物块的运动过程,A到B的过程为平抛运动,已知高度运用平抛运动的规律求出时间;(2)知道运动过程中能量的转化,弹簧的弹性势能转化给物块的动能;(3)从A点到最后停在轨道CD上的某点p,物块的动能和重力势能转化给摩擦力做功产生的内能.
【考点精析】掌握平抛运动和功能关系是解答本题的根本,需要知道特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;当只有重力(或弹簧弹力)做功时,物体的机械能守恒;重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2;合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 (动能定理);除了重力(或弹簧弹力)之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1.