Question

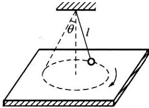如图所示，长为l的绳子下端连着质量为m的小球，上端悬于天花板上，当把绳子拉直时，绳子与竖直线夹角为60°，此时小球静止于光滑水平桌面上．
（1）当球以ω=

g l

做圆锥摆运动时，绳子张力T为多大？桌面受到压力N为多大？
（2）当球以角速度ω=

4g l

做圆锥摆运动时，绳子的张力及桌面受到的压力各为多少？

Answer 1

分析：（1）当球做圆锥摆运动时，小球在水平面内做匀速圆周运动，由重力、水平面的支持力和绳子拉力的合力提供向心力，根据牛顿第二定律，采用正交分解法列方程求解绳子的张力和支持力，再由牛顿第三定律求出桌面受到的压力．
（2）当小球对桌面恰好无压力时，由重力和绳子拉力的合力提供向心力，根据牛顿第二定律求解此时小球的角速度．根据角速度ω=

4g l

与临界角速度的关系，判断小球是否离开桌面．若小球桌面做圆周运动，再由牛顿第二定律求解绳子的张力．

解答：解：（1）对小球受力分析，作出力图如图1．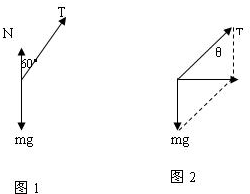
根据牛顿第二定律，得
   Tsin60°=mω²Lsin60°①
   mg=N+Tcos60°  ②
又ω=

g l

解得
   T=mg，N=

1

2

mg
（2）设小球对桌面恰好无压力时角速度为ω₀，即N=0
代入①②得ω₀=

2g L

由于ω=

4g l

＞ω₀，故小球离开桌面做匀速圆周运动，则N=0此时小球的受力如图2．设绳子与竖直方向的夹角为θ，则有
  mgtanθ=mω²?Lsinθ③
   mg=Tcosθ        ④
联立解得  T=4mg
答：
（1）当球以ω=

g l

做圆锥摆运动时，绳子张力T=mg，桌面受到压力N=

1

2

mg；
（2）当球以角速度ω=

4g l

做圆锥摆运动时，绳子的张力为4mg，桌面受到的压力为零．

点评：本题是圆锥摆问题，分析受力，确定向心力来源是关键，实质是牛顿第二定律的特殊应用．