Question

【题目】如图所示，在水平面上有两条光滑平行金属导轨MN、PQ，导轨间距为L，匀强磁场的磁感应强度大小为B，方向垂直导轨平面向里。两根完全相同的金属杆1、2间隔一定的距离摆放在导轨上，且与导轨垂直，它们的电阻均为R，两导轨电阻不计。杆1以初速度滑向杆2，为使两杆不相碰，则在杆2固定与不固定两种情况下，下列说法正确的是：

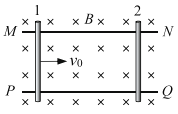
A. 杆2不固定时，两杆组成的系统动量守恒。

B. 两种情况下，最初两杆最小间距之比1：2

C. 两种情况下，最初两杆最小间距之比2：1

D. 在题设两种情况下，通过闭合回路的电荷量之比4：1

Answer 1

【答案】AC

【解析】

两个棒均不固定时，左边棒受向左的安培力，右边棒受向右的安培力，故左边棒减速，右边棒加速，两个棒系统动量守恒，根据动量守恒定律得到最后的共同速度，然后对右边棒运用动量定理列式；当右边棒固定时，左边棒受向左的安培力，做减速运动，根据动量定理列式；最后联立求解即可。

A.两个棒均不固定时，左边棒受向左的安培力，右边棒受向右的安培力，系统所受的合力为零，则系统的动量守恒，选项A正确；

BC.金属杆1、2均不固定时，系统动量守恒，以向右为正方向，有：mv0=2mv，解得：；对右侧杆，采用微元法，以向右问正方向，根据动量定理，有：∑-F△t=∑m△v，其中：F=BIL=BL，故：-∑△t=∑m△v，即=m，解得：l1-l2=，即AB间的距离最小为x=；当棒2固定后，对左侧棒，以向右为正方向，根据动量定理，有：∑-F△t=∑m△v，其中：F=BIL=BL，故：-∑△t=∑m△v，即-=-mv0，解得：，故AB间的距离最小为x′=；故x′：x=2：1；故B错误，C正确；

D.根据可知，因x′：x=2：1，则两种情况下，通过闭合回路的电荷量之比2：1，选项D错误；

故选AC。