题目内容
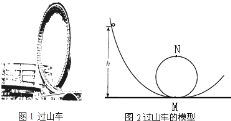
【题目】游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来（如图1）．我们把这种情况抽象为图2的模型：弧形轨道的下端与竖直圆轨道相接，使小球从弧形轨道上端无初速滚下，小球进入圆轨道下端后沿圆轨道运动，其中M、N分别为圆轨道的最低点和最高点．实验发现，只要h大于一定值，小球就可以顺利通过圆轨道的最高点．如果已知圆轨道的半径为R=5.0m小球质量为m=1.0kg（不考虑摩擦等阻力）则：
A. 小球恰过最高点时重力提供向心力
B. 要使小球恰过最高点，h为12.5m
C. h小于12.5m时小球一定脱轨运动
D. 要使小球不脱离轨道运动h必须大于12.5m
【答案】AB
【解析】
AB、小球恰能通过N点，即小球通过最高点时恰好不受轨道的压力，重力提供向心力，即应满足：
，解得：
，小球运动到最高点的过程中，只有重力做功，由机械能守恒定律：
，解得：
，故A、B正确；
CD、当刚好到到四分之一圆周，只有重力做功，由机械能守恒定律：
，解得：
，要使小球不脱离轨道运动，则有可能越过最高点或可能不越过四分之一圆周，即h不大于5m或不小于12.5m，故C、D错误；
故选AB。
练习册系列答案
相关题目
