题目内容
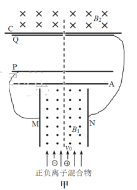
【题目】如图所示，两条相互平行的光滑金属导轨，相距L=0.2m，左侧轨道的倾斜角θ=30°，右侧轨道为圆弧线，轨道端点间接有电阻R=1.5Ω，轨道中间部分水平，在MP、NQ间有距离为d=0.8m，宽与导轨间距相等的方向竖直向下的匀强磁场。磁感应强度B随时间变化如图乙所示。一质量为m=10g、导轨间电阻为r=1.0Ω的导体棒a从t=0时刻无初速释放，初始位置与水平轨道间的高度差H=0.8m。另一与a棒完全相同的导体棒b静置于磁场外的水平轨道上，靠近磁场左边界PM。a棒下滑后平滑进入水平轨道（转角处无机械能损失），并与b棒发生碰撞而粘合在一起，此后作为一个整体运动。导体棒始终与导轨垂直并接触良好，轨道的电阻和电感不计,g取10m/s2。求：
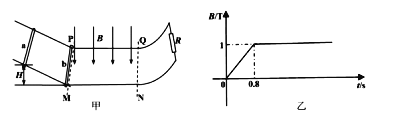
（1）a导体棒进入磁场前瞬间速度大小和a导体棒从释放到进入磁场前瞬间过程中所用的时间
（2）粘合导体棒刚进入磁场瞬间受到的安培力大小
（3）粘合导体棒最终静止的位置离PM的距离
（4）全过程电阻R上产生的焦耳热
【答案】（1）4m/s；t=0.8s（2）F=0.04N（3）停在距离PM为0.4m处（4）0.042J
【解析】
（1）设a导体棒进入磁场前瞬间速度大小为v
a导体棒从释放到进入磁场前瞬间过程中由机械能守恒定律有：
解得：v=4m/s
a导体棒从释放到进入磁场前瞬间过程由牛顿第二定律有：
解得：a=5m/s2
由速度与时间的关系式v=at解得t=0.8s
（2）a与b发生完全非弹性碰撞后的速度为v
由动量守恒定律有：mv=（m+m）v
解得：v=2m/s
此时粘合导体棒刚好进入匀强磁场，安培力为：F=BIL，
，E=BLv，解得：F=0.04N
（3）粘合导体棒直到静止，由动量定理有：-BILt=0-2mv，
=It，
解得：
因此粘合导体棒停在距离PM为0.4m处
（4）导体棒滑入磁场前，由法拉第电磁感应定律可知：
由闭合电路欧姆定律有：
有：
=0.012J
碰撞后回路产生的热量Q=
×2mv2=QR2+Qr
代入数据解得：QR2=0.03J
整个过程中，电阻R上产生的焦耳热为：QR=QR1+QR2=0.042J
