��Ŀ����
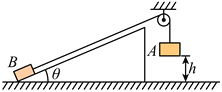
����Ŀ����ͼ��ʾ��һ��L��16m��ˮƽ���ʹ�����v��10m/s����������˳ʱ��ת������һ����Ϊm��1kg��������ٶȵ�����ڴ��ʹ���ˣ�����봫�ʹ�֮��Ķ�Ħ�������̣�0.5��ȡg��10m/s2����

��1������ڴ��ʹ��ϴ�����˶����Ҷ˵�ʱ�䡣
��2�����ô��ʹ�װ����ˮƽ������ȣ�37����ǣ���ͬ��������˳ʱ��ת��������������ٶȵط��ϴ��ʹ����ˣ��������������Ӵ��ʹ��϶��˶����¶˵�ʱ�䡣
���𰸡���1��2.6s����2��2s
��������
��1������ţ�ٵڶ����������ٶȣ����ﵽ�봫�ʹ�����ʱ��ʱ����»��ľ������Ժ���������˶������ݹ�ʽ���ʱ����
��2���ڶ����ͷź���ţ�ٵڶ����������ٶȣ��ﵽ�����ͬ�ٶȺ����������٣�Ħ��������ı䣬�ٴ������ٶȼ��ɣ�����˶���ʽ�����ʱ����
��1��������ϴ��ʹ�����ţ�ٵڶ����ɣ���mg=ma
a=��g=5m/s2
�ܴﵽ���٣���ʱ��![]() ��
��
s=![]() t1=10m��L֮�����٣�
t1=10m��L֮�����٣�
������һ�˵�ʱ��![]()
���Թ���ʱ��t=t1+t2=2.6s��
��2���ڶ����ͷź�mgsin��+��mgcos��=ma1
�������ݽ�ã�a1=10m/s2����������
�ﵽ�����ͬ�ٶ�ʱ����ʱ��![]()
s=![]() =5m��L
=5m��L
֮����Ϊ�̣�tg��=0.75�����������٣�
����ţ�ٵڶ����ɣ�mgsin��-��mgcos��=ma2
��ã�a2=2m/s2���������£�
����![]() ��
��![]()
���t2��=1s����ֵ�����
����ʱ��![]()

 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�