题目内容
【题目】如图,三角形ABC为某透明介质的横截面,O为BC边的中点,位于截面所在平面内的一束光线自O以角I入射,第一次到达AB边恰好发生全反射,已知θ=15°,BC边长为2L,该介质的折射率为![]() ,求:
,求:

(i)入射角i;
(ii)从入射角到发生第一次全反射所用的时间(设光在真空中的速度为v,可能用到sin75°=![]() 或sin15°=2﹣
或sin15°=2﹣![]() )
)
【答案】(i)45°;
(ii)t=![]() L
L
【解析】
试题由全反射定律求出临界角,由几何关系得到光线在BC面上的折射角,折射定律得到入射角;
根据正弦定理求出光线在介质中路程,由v=![]() 求出玻璃中的传播速度,进而求出所用时间.
求出玻璃中的传播速度,进而求出所用时间.
解:(i)根据全反射定律可知,光线在AB面上的P点的入射角等于临界角C,由折射定律得: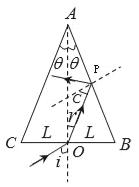
sinC=![]()
代入数据得:
C=45°
设光线在BC面上的折射角为r,由几何关系得:γ+C=90°﹣θ
所以:r=30°
n=![]()
联立得:i=45°
(ii)在△OPB中,根据正弦定理得:
![]() =
=![]()
设所用时间为t,光线在介质中的速度为v,得:OP=VT
v=![]()
联立得:t=![]() L
L
答:(i)入射角i为45°;
(ii)从入射角到发生第一次全反射所用的时间t=![]() L.
L.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目