题目内容
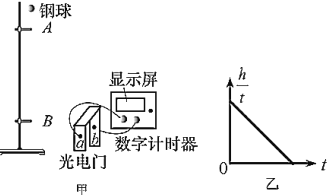
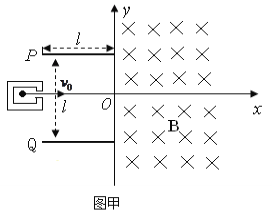
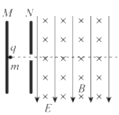
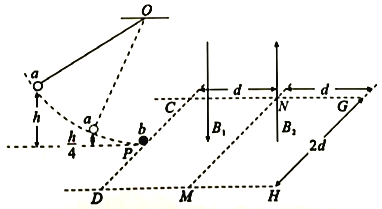
【题目】如图所示，在光滑绝缘水平面上，存在两个相邻的相同矩形区域CDMN和NMHG，，CD=NM=GH=2d、CN=NG=d．区域CDMN中存在方向竖直向下的匀强磁场B1，区域MMHG中存在方向竖直向上的匀强磁场B2。不可伸长的轻质细线，一端固定于O点，另一端拴有一个质量为
的绝缘小球a。拉紧细线使小球a从距离桌面高h的位置静止释放，当小球a沿圆弧运动至悬点正下方位置时，与静止于该处的带正电小球b发生正碰，碰后小球a向左摆动，上升的最大高度为
，小球b从CD边界中点P垂直进入CDMN区域，已知小球b质量为m，带电量为+q，且始终保持不变，重力加速度为g。则
(1)通过计算判断a、b两小球的碰撞是否为弹性碰撞；
(2)若B1=B2=B，要使b小球能从NG边界射出，求B的取值范围；
(3)若区域CDMN中磁感应强度B1=
，方向仍竖直向下。将区域NMHG中磁场改为匀强电场，电场方向水平且由N指向M。是否存在一个大小合适的场强使小球b恰由H点离开电场区域，若存在请算出场强E的大小，不存在请说明理由。
【答案】(1)弹性碰撞，分析过程见解析；(2)
；(3)存在，
。
【解析】
(1)设小球a碰前的速率为
，碰后速率为
，小球b的速率为
，a小球与b小球碰撞前：
①
a小球与b小球碰撞后：
②
a小球与b小球碰撞时，以水平向右为正方向：
③
联立①②③得：
碰撞前两物体总动能
碰撞后两物体总动能
碰撞前后总动能守恒，所以a、b两小球碰撞属于弹性碰撞。
(2)若小球b恰好从N点射出，作出小球的运动轨迹，如图所示。由几何关系得：
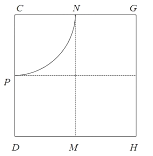
R=d④
而
⑤
联立解得：
；
若小球b恰好从G点射出，作出小球的运动轨迹，如图所示。
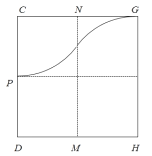
由几何关系可得：
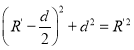⑥
⑦
联立解得：
综上可得B的取值范围为：
；
(3)由(2)可得当
小球b在CDMN区域里做圆周运动后小球从距离N点
处以速度vb斜射入MNGH区域中，设vb与边界NM夹角为θ，由几何关系得：
由运动合成分解可知：
假设小球恰好能从H点离开电场，运动时间为t。x轴方向做匀速直线运动，y轴方向做类竖直上抛运动。
x=d
x=vxt⑧
⑨
（以电场相反方向为正方向）
⑩
联立解得：
令vy减为0时，小球沿y轴向上的最大位移
小球未从NG边界离开电场区域。
故假设成立，即电场强度 时小球恰能从H点离开。
