题目内容
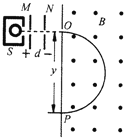
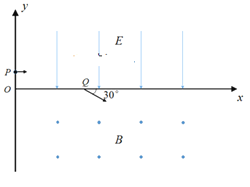
【题目】如图所示的xoy坐标系中，在第I象限内存在沿y轴负向的匀强电场，第IV象限内存在垂直纸面向外的匀强磁场。一个比荷q/m=102c/kg的带正电粒子从y轴上的P点垂直进入匀强电场，经过x轴上的Q点以速度v=2m/s进入磁场，方向与x轴正向成30°。若粒子在磁场中运动后恰好能再回到电场，已知OQ长L=6m，粒子的重力不计，电场强度E和磁感应强度B大小均未知。求：
(1)OP的距离
(2)磁感应强度B的大小
(3)若在O点右侧44m处放置一平行于y轴的挡板，粒子能击中挡板并被吸收，求粒子从P点进入电场到击中挡板的时间.
【答案】(1)
(2) B=5×10-3T (3)
【解析】
(1)粒子在电场中做类平抛运动，根据平行四边形定则求出粒子在沿电场方向和垂直电场方向上的速度，结合运动学公式求出OP间的距离；
(2)粒子恰好能再回到电场，结合几何关系求出临界半径，结合半径公式求出磁感应强度的大小；
(3)根据几何关系求出一个周期内在x轴上发生的距离，确定出粒子能完成周期运动的次数．结合在电场中和磁场中运动的时间，以及最后2L内的时间求出粒子从P点进入电场到击中挡板的时间。
(1) 粒子在Q点进入磁场时，vx=vcos30°，
vy=vsin30°，
粒子从P点运动到Q点时间
t=L/vx
OP间距离
解得：
；
(2) 粒子恰好能回到电场，即粒子在磁场中轨迹的左侧恰好与y轴相切，设半径为R
R+Rsin30°=L
联立解得：B=5×10-3T ；
(3) 粒子在电场和磁场中做周期性运动，轨迹如图
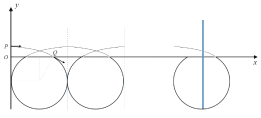
一个周期运动过程中，在x轴上发生的距离为
△L=L+L-2Rsin30°=8m
P点到挡板的距离为44m，所以粒子能完成5个周期的运动，然后在电场中沿x轴运动4m时击中挡板。
5个周期的运动中，在电场中的时间为
磁场中运动的时间
剩余2L中的运动时间
总时间 
。
