题目内容
7. 如图两摆摆长相同,悬挂于同一高度,A、B两摆球体积均很小,当两摆均处于自由静止状态时,其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成60°角,然后将其由静止释放.在最低点两摆球粘在一起摆动,且最大摆角成37°,忽略空气阻力.求:
如图两摆摆长相同,悬挂于同一高度,A、B两摆球体积均很小,当两摆均处于自由静止状态时,其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成60°角,然后将其由静止释放.在最低点两摆球粘在一起摆动,且最大摆角成37°,忽略空气阻力.求:①A球和B球质量之比
②两球在碰撞过程中损失的机械能与B球在碰前的最大动能之比.
分析 先根据机械能守恒求出小球B摆到最低点与A碰撞前瞬间的速度大小.根据两摆球粘在一起摆动,且最大摆角成37°,求解撞后瞬间的速度大小,再根据动量守恒求解.
根据能量守恒求出损失的机械能,再进行求解损失的机械能与B球在碰前的最大动能之比.
解答 解:(1)向右上方拉动B球使其摆线伸直并与竖直方向成60°角,向下摆动的过程,机械能守恒,则有:
mg×$\frac{L}{2}$=$\frac{1}{2}$mv2
v=$\sqrt{gL}$,
两摆球粘在一起摆动,且最大摆角成37°,
机械能守恒,则有:
m′g×0.2L=$\frac{1}{2}$m′v′2
v′=2$\sqrt{L}$,
B球与A球碰撞,粘在一起,规定向左为正方向,根据动量守恒得
mBv=(mA+mB)v′
解得:$\frac{{m}_{A}}{{m}_{B}}$=$\frac{\sqrt{10}-2}{2}$,
(2)B球在碰前的最大动能是Ek=$\frac{1}{2}$mBv2=$\frac{1}{2}$mBgL=5mBL
两球在碰撞过程中损失的机械能△E=$\frac{1}{2}$mBgL-$\frac{1}{2}$(mA+mB)v′2=(5-$\sqrt{10}$)mBL
所以两球在碰撞过程中损失的机械能与B球在碰前的最大动能之比是$\frac{5-\sqrt{10}}{5}$,
答:①A球和B球质量之比是$\frac{\sqrt{10}-2}{2}$,
②两球在碰撞过程中损失的机械能与B球在碰前的最大动能之比是$\frac{5-\sqrt{10}}{5}$.
点评 本题考查了求物体的速度,分析清楚物体运动过程,选择恰当的研究对象与过程,应用机械能守恒与动量守恒定律可以正确解题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
17.把火星和地球绕太阳运行的轨道视为圆周,由火星和地球绕太阳运行的周期之比可求得( )
| A. | 火星和地球的质量之比 | B. | 火星和太阳的质量之比 | ||
| C. | 火星和地球到太阳的距离之比 | D. | 火星和地球表面的重力加速度之比 |
18.用X粒子轰击铝27(${\;}_{13}^{27}$Al),产生钠24(${\;}_{11}^{24}$Na)和α粒子.钠24具有放射性,可以进行人体血液循环的示踪实验,达到医学诊断的目的,它衰变后变成镁24(${\;}_{12}^{24}$Mg).则下列正确的是( )
| A. | X粒子是质子 | B. | 钠24发生的是α衰变 | ||
| C. | X粒子是中子 | D. | 钠24发生的衰变对人没有一点害处 |
15.下列说法中正确的是( )
| A. | 气体压强的大小和单位体积内的分子数及气体分子的平均动能都有关 | |
| B. | 布朗运动是液体分子的运动,说明液体分子永不停息地做无规则热运动 | |
| C. | 热力学第二定律的开尔文表述:不可能从单一热库吸收热量,使之完全变成功,而不产生其他影响 | |
| D. | 水黾可以停在水面上是因为液体具有表面张力 | |
| E. | 温度升高,物体所有分子的动能都增大 |
2.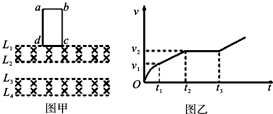 如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1与L2和L3与L4之间存在匀强磁场,磁感应强度大小均为1T,方向垂直于虚线所在平面向里.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,t2~t3之间图线为与t轴平行的直线,t1~t2之间和t3之后的图线均为倾斜直线,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向(重力加速度g取10m/s2)则( )
如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1与L2和L3与L4之间存在匀强磁场,磁感应强度大小均为1T,方向垂直于虚线所在平面向里.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,t2~t3之间图线为与t轴平行的直线,t1~t2之间和t3之后的图线均为倾斜直线,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向(重力加速度g取10m/s2)则( )
 如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1与L2和L3与L4之间存在匀强磁场,磁感应强度大小均为1T,方向垂直于虚线所在平面向里.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,t2~t3之间图线为与t轴平行的直线,t1~t2之间和t3之后的图线均为倾斜直线,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向(重力加速度g取10m/s2)则( )
如图甲所示,在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4,在L1与L2和L3与L4之间存在匀强磁场,磁感应强度大小均为1T,方向垂直于虚线所在平面向里.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2Ω,将其从图示位置静止释放(cd边与L1重合),速度随时间的变化关系如图乙所示,t1时刻cd边与L2重合,t2时刻ab边与L3重合,t3时刻ab边与L4重合,t2~t3之间图线为与t轴平行的直线,t1~t2之间和t3之后的图线均为倾斜直线,已知t1~t2的时间间隔为0.6s,整个运动过程中线圈平面始终处于竖直方向(重力加速度g取10m/s2)则( )| A. | 在0~t1时间内,通过线圈的电荷量为2.5C | |
| B. | 线圈匀速运动的速度大小为8m/s | |
| C. | 线圈的长度为2m | |
| D. | 0~t3时间内,线圈产生的热量为4.2J |
12.某课外兴趣小组用铜片和锌片插入苹果中,组成了一个苹果电池,并用“测定电动势和内电阻”的实验方法测定该苹果电池的电动势和内电阻.
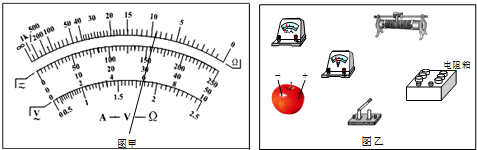
(1)实验前,甲同学利用调好的多用电表欧姆“×100”档来粗测该苹果电池的内阻.测量结果如图甲所示.他这样做是否正确?若正确,请读出其内阻值;若不正确,请说明理由.不正确 水果电池为电源,欧姆表不能电源的内阻.
(2)乙同学设计好测量电路,选择合适的器材,得到苹果电池两端的电压U和流过它的电流I的几组数据,如下表所示.
①请根据第2组和第5组数据计算得到该苹果电池的电动势E=1.00V;内电阻r=1.06kΩ.(结果保留两位小数).
②除苹果电池、电压表、电流表、电键、导线若干外,可供选择的实验器材有:滑动变阻器R1(阻值0~10Ω);电阻箱R2(阻值0~9999.9Ω),该电路中可变电阻应选择R2(选填R1或R2)
②请选择合适器材用铅笔划线代替导线将图乙中实物连接完整.

(1)实验前,甲同学利用调好的多用电表欧姆“×100”档来粗测该苹果电池的内阻.测量结果如图甲所示.他这样做是否正确?若正确,请读出其内阻值;若不正确,请说明理由.不正确 水果电池为电源,欧姆表不能电源的内阻.
(2)乙同学设计好测量电路,选择合适的器材,得到苹果电池两端的电压U和流过它的电流I的几组数据,如下表所示.
| 数据序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.85 | 0.81 | 0.75 | 0.68 | 0.62 | 0.54 |
| I/mA | 0.14 | 0.18 | 0.24 | 0.32 | 0.36 | 0.48 |
②除苹果电池、电压表、电流表、电键、导线若干外,可供选择的实验器材有:滑动变阻器R1(阻值0~10Ω);电阻箱R2(阻值0~9999.9Ω),该电路中可变电阻应选择R2(选填R1或R2)
②请选择合适器材用铅笔划线代替导线将图乙中实物连接完整.
16.丹麦物理学家奥斯特在1820年发现了电流的磁效应,奥斯特在实验中,将直导线沿南北方向水平放置,指针靠近直导线,下列结论正确的是( )
| A. | 把小磁针放在导线的延长线上,通电后小磁针会转动 | |
| B. | 把小磁针平行地放在导线的下方,通电后小磁针不会立即发生转动 | |
| C. | 把小磁针平行地放在导线的下方,给导线通以恒定电流,然后逐渐增大导线与小磁针之间的距离,小磁针转动的角度(与通电前相比)会逐渐增大 | |
| D. | 把黄铜针(用黄铜制成的指针)平行地放在导线的下方,通电后黄铜针一定会转动 |
17.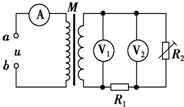 如图所示,M是小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接正弦交变电源,电压u=311sin 100πt(V).变压器右侧部分为火警系统原理图,其中R2为半导体热敏材料制成的传感器,其电阻随温度升高而减小;R1为定值电阻.下列说法正确的是( )
如图所示,M是小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接正弦交变电源,电压u=311sin 100πt(V).变压器右侧部分为火警系统原理图,其中R2为半导体热敏材料制成的传感器,其电阻随温度升高而减小;R1为定值电阻.下列说法正确的是( )
 如图所示,M是小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接正弦交变电源,电压u=311sin 100πt(V).变压器右侧部分为火警系统原理图,其中R2为半导体热敏材料制成的传感器,其电阻随温度升高而减小;R1为定值电阻.下列说法正确的是( )
如图所示,M是小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接正弦交变电源,电压u=311sin 100πt(V).变压器右侧部分为火警系统原理图,其中R2为半导体热敏材料制成的传感器,其电阻随温度升高而减小;R1为定值电阻.下列说法正确的是( )| A. | 电压表V1的示数为31.1V | |
| B. | 变压器副线圈中电流的频率为25Hz | |
| C. | 当R2所在处出现火警时,电压表V2的示数变小,电流表A的示数变大 | |
| D. | 当R2所在处出现火警时,变压器原线圈的输入功率变小 |