题目内容
17.把火星和地球绕太阳运行的轨道视为圆周,由火星和地球绕太阳运行的周期之比可求得( )| A. | 火星和地球的质量之比 | B. | 火星和太阳的质量之比 | ||
| C. | 火星和地球到太阳的距离之比 | D. | 火星和地球表面的重力加速度之比 |
分析 研究火星和地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式表示出周期.
根据圆周运动知识表示出周期.
解答 解:A、我们研究火星和地球绕太阳做圆周运动,火星和地球作为环绕体,无法求得火星和地球的质量之比,故A错误;
B、根据题目已知条件,不能求得火星和太阳的质量之比,故B错误;
C、研究火星和地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
得T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,其中M为太阳的质量,r为轨道半径.
火星和地球绕太阳运动的周期之比为$\sqrt{\frac{{r}_{火}^{3}}{{r}_{地}^{2}}}$,所以能求得火星和地球到太阳的距离之比,故C正确;
D、根据万有引力等于重力得g=$\frac{GM}{{R}^{2}}$,由于星球的半径之比不知道,故不可以求得火星和地球绕太阳运动的表面的重力加速度之比,故D错误.
故选:C.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
相关题目
7.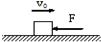 如图所示,放在光滑水平面上的木块以速率v0向右做匀速直线运动.现有一随时间从零开始做线性变化的水平力F向左作用在木块上,在这个过程中,以向右为正方向,能正确描述木块运动的v-t图线是图中的( )
如图所示,放在光滑水平面上的木块以速率v0向右做匀速直线运动.现有一随时间从零开始做线性变化的水平力F向左作用在木块上,在这个过程中,以向右为正方向,能正确描述木块运动的v-t图线是图中的( )
 如图所示,放在光滑水平面上的木块以速率v0向右做匀速直线运动.现有一随时间从零开始做线性变化的水平力F向左作用在木块上,在这个过程中,以向右为正方向,能正确描述木块运动的v-t图线是图中的( )
如图所示,放在光滑水平面上的木块以速率v0向右做匀速直线运动.现有一随时间从零开始做线性变化的水平力F向左作用在木块上,在这个过程中,以向右为正方向,能正确描述木块运动的v-t图线是图中的( )| A. | 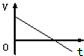 | B. | 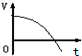 | C. | 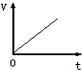 | D. | 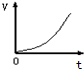 |
8.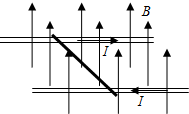 如图所示,一导体棒放置在处于匀强磁场中的两条平行金属导轨上,并与金属导轨组成闭合回路.当回路中通有电流I时,导体棒会受到安培力作用.如要使安培力增大,则以下方法正确的为 ( )
如图所示,一导体棒放置在处于匀强磁场中的两条平行金属导轨上,并与金属导轨组成闭合回路.当回路中通有电流I时,导体棒会受到安培力作用.如要使安培力增大,则以下方法正确的为 ( )
 如图所示,一导体棒放置在处于匀强磁场中的两条平行金属导轨上,并与金属导轨组成闭合回路.当回路中通有电流I时,导体棒会受到安培力作用.如要使安培力增大,则以下方法正确的为 ( )
如图所示,一导体棒放置在处于匀强磁场中的两条平行金属导轨上,并与金属导轨组成闭合回路.当回路中通有电流I时,导体棒会受到安培力作用.如要使安培力增大,则以下方法正确的为 ( )| A. | 增大磁感应强度 | B. | 使磁感应强度反向 | ||
| C. | 使电流强度反向 | D. | 减小电流强度 |
12.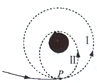 “嫦娥”三号探测器发射到月球上经过多次变轨,最终降落到月球表面上,其变轨示意图如图所示,其中圆形轨道I上的P点即为椭圆轨道Ⅱ的远月点.则探测器( )
“嫦娥”三号探测器发射到月球上经过多次变轨,最终降落到月球表面上,其变轨示意图如图所示,其中圆形轨道I上的P点即为椭圆轨道Ⅱ的远月点.则探测器( )
 “嫦娥”三号探测器发射到月球上经过多次变轨,最终降落到月球表面上,其变轨示意图如图所示,其中圆形轨道I上的P点即为椭圆轨道Ⅱ的远月点.则探测器( )
“嫦娥”三号探测器发射到月球上经过多次变轨,最终降落到月球表面上,其变轨示意图如图所示,其中圆形轨道I上的P点即为椭圆轨道Ⅱ的远月点.则探测器( )| A. | 在轨道I运行时的加速度大于月球表面的重力加速度 | |
| B. | 分别经过轨道Ⅰ、Ⅱ上的P点时的加速度大小相等 | |
| C. | 在轨道I的运行周期比在轨道Ⅱ的小 | |
| D. | 在P点由轨道I进人轨道Ⅱ必须点火加速 |
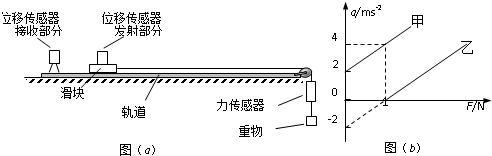

 如图两摆摆长相同,悬挂于同一高度,A、B两摆球体积均很小,当两摆均处于自由静止状态时,其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成60°角,然后将其由静止释放.在最低点两摆球粘在一起摆动,且最大摆角成37°,忽略空气阻力.求:
如图两摆摆长相同,悬挂于同一高度,A、B两摆球体积均很小,当两摆均处于自由静止状态时,其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成60°角,然后将其由静止释放.在最低点两摆球粘在一起摆动,且最大摆角成37°,忽略空气阻力.求: