题目内容
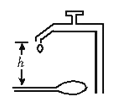
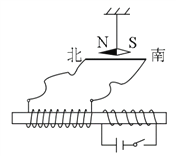
【题目】如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ。粗细均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直固定在倾斜导轨上。空间有方向竖直的匀强磁场(图中未画出)。两金属棒与导轨保持良好接触。不计所有导轨和ab棒的电阻,ef棒的阻值为R,忽略感应电流产生的磁场,重力加速度为g。

(1)若磁感应强度大小为B,给ab棒一个垂直于NQ、水平向右的速度v1,在水平导轨上沿运动方向滑行一段距离后停止,ef棒始终静止,求此过程ef棒上产生的热量;
(2)在(1)问过程中,ab棒滑行距离为d,求通过ab棒某横截面的电量。
【答案】(1)![]() mv12(2)
mv12(2)![]()
【解析】(1)ab棒在水平导轨上运动的过程,根据能的转化与守恒定律,有: ![]() mv12=QR+Qef①
mv12=QR+Qef①
由于金属棒ab和ef的电阻相等,电阻R和ef棒中产生的焦耳热相等,则 QR=Qef②
由①②式联立解得ef棒上产生的热量为:Qef=![]()
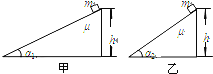
(2)设在ab棒滑行距离为d时所用时间为t,其示意图如下图所示: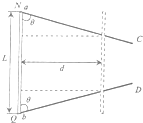
该过程中回路变化的面积为:△S=![]() [L+(L-2dcotθ)]d③
[L+(L-2dcotθ)]d③
在该过程中,回路平均感应电动势为: ![]() ④
④
流经ab棒平均电流为: ![]() ⑤
⑤
流经ab棒某横截面的电量为:q=![]() t⑥
t⑥
由③④⑤⑥式联立解得: ![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目