��Ŀ����
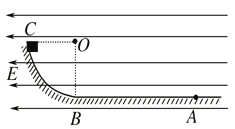
����Ŀ����ͼ��ʾ��ˮƽ���õ��������ԵĴ��������MN��PQ��������ֱ����ǿ�糡����ǿ�ų����糡ǿ��ΪE���Ÿ�Ӧǿ��ΪB����a���ɾ�ֹ�ͷ�һ������������ͷź���������acb�˶�������b��ʱ�ٶ�Ϊ�㣬c������������MN����Զ�ĵ㡣��֪��������Ϊm�������Ϊq���������ٶ�Ϊg�����������ܿ���������������˵������ȷ����

A������a��ʱ���ٶȷ�����ֱ����
B������c��ʱ���������
C�����˶������е��������Ϊ![]()
D��������b�����ԭ·������a��
���𰸡�A
��������
�������������a��ʱ���ٶ�Ϊ0������������Ϊ0�����ܵ���������糡���ķ��������µģ��ʴ�ʱ���ļ��ٶȷ�����ֱ���£�ѡ��A��ȷ��������a�˶���c��ʱ���糡���������������ܼ�С��������c��ĵ�������С��ѡ��B��������c��ʱ�Ķ�������ٶ�������ѡ��C��ȷ�������mg+Eq=Bqv����˵����c��ʱ�ܵ����������糡��������������ƽ��ģ���������c�������������˶�������������ֱ���ϣ���������������ƽ����������ʽ�Dz������ģ�ѡ��C����������b���������˶����ֻ��ܵ����ҵ�����������������������ƫת����������ԭ·���ص�a�㣬ѡ��D����

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�