题目内容
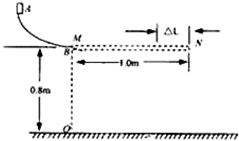 如图所示,竖直平面内有一光滑的
如图所示,竖直平面内有一光滑的| 1 | 4 |
(1)滑至B点时圆弧轨道对滑块的支持力.
(2)在B端接一长为1.0m的木板MN,滑块从A点释放后正好落在N端正下方的P点(图中未标出),求木板与滑块的动摩擦因数.
(3)若将木板右端截去长为△L的一段,仍从A端释放滑块,请通过计算判断最终的落点在P点左侧还是右侧?(要求写出计算过程)
分析:(1)滑块从光滑圆弧下滑过程中,只有重力做功,滑块的机械能守恒,根据机械能守恒定律列式求解B点速度;在B点,根据重力和支持力的合力提供向心力列式求解支持力,再结合牛顿第三定律得到压力;滑块从B到C过程中做平抛运动,根据平抛运动的分位移公式列式求解;
(2)滑块落在N端正下方说明它到N点的速度刚好为0,从M到N,滑动摩擦力对滑块做负功,根据动能定理求出木板与滑块的动摩擦因数;
(3)若将木板右端截去长为△L的一段,根据动能定理求出滑块滑到木板右端的速度,由平抛运动知识得出落地点距O点的距离与△L的关系,由数学知识分析.
(2)滑块落在N端正下方说明它到N点的速度刚好为0,从M到N,滑动摩擦力对滑块做负功,根据动能定理求出木板与滑块的动摩擦因数;
(3)若将木板右端截去长为△L的一段,根据动能定理求出滑块滑到木板右端的速度,由平抛运动知识得出落地点距O点的距离与△L的关系,由数学知识分析.
解答:解:(1)滑块从光滑圆弧下滑过程中,根据机械能守恒定律得
mgR=
m
解得,vB=
=
m/s=3m/s
在B点,重力和支持力的合力提供向心力,根据牛顿第二定律,有:
N-mg=m
解得:N=3mg=3N;
(2)由题意,要使滑块落在N端正下方说明它到N点的速度刚好为0,从M到N,根据动能定理得:
-μmgL=0-
m
解得,μ=
=
=0.45
(3)若将木板右端截去长为△L的一段后,设滑块滑到木板最右端时速度为v,由动能定理得
-μmg(L-△L)=
mv2-
m
则得,v
=
=3
滑块离开木板后做平抛运动,高度决定运动时间,则得:
h=
gt2
得,t=
=
s=0.4s
所以水平位移为 x=vt=3
×0.4m=1.2
因为
=
=
因△L<1,则得
>1
可知,滑块最终的落点在P点右侧.
答:
(1)滑至B点时圆弧轨道对滑块的支持力是3N.
(2)木板与滑块的动摩擦因数是0.45.
(3)若将木板右端截去长为△L的一段,仍从A端释放滑块,滑块最终的落点在P点右侧.
mgR=
| 1 |
| 2 |
| v | 2 B |
解得,vB=
| 2gR |
| 2×10×0.45 |
在B点,重力和支持力的合力提供向心力,根据牛顿第二定律,有:
N-mg=m
| ||
| R |
解得:N=3mg=3N;
(2)由题意,要使滑块落在N端正下方说明它到N点的速度刚好为0,从M到N,根据动能定理得:
-μmgL=0-
| 1 |
| 2 |
| v | 2 B |
解得,μ=
| ||
| 2gL |
| 32 |
| 2×10×1 |
(3)若将木板右端截去长为△L的一段后,设滑块滑到木板最右端时速度为v,由动能定理得
-μmg(L-△L)=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 B |
则得,v
|
| 9-2×0.45×10×(1-△L) |
| △L |
滑块离开木板后做平抛运动,高度决定运动时间,则得:
h=
| 1 |
| 2 |
得,t=
|
|
所以水平位移为 x=vt=3
| △L |
| △L |
因为
| x |
| △L |
1.2
| ||
| △L |
| 1.2 | ||
|
因△L<1,则得
| x |
| △L |
可知,滑块最终的落点在P点右侧.
答:
(1)滑至B点时圆弧轨道对滑块的支持力是3N.
(2)木板与滑块的动摩擦因数是0.45.
(3)若将木板右端截去长为△L的一段,仍从A端释放滑块,滑块最终的落点在P点右侧.
点评:此题是机械能守恒、牛顿第二定律、动能定理和平抛运动的综合,关键掌握每个过程遵守的物理规律,运用程序法按顺序求解.

练习册系列答案
相关题目
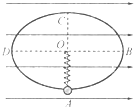 如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心O,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的匀强电场中.将小环从A点由静止释放,小环运动到B点时速度恰好为0.已知小环在A、B两点时弹簧的弹力大小相等,则( )
如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心O,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的匀强电场中.将小环从A点由静止释放,小环运动到B点时速度恰好为0.已知小环在A、B两点时弹簧的弹力大小相等,则( )| A、小环从A点运动到B点的过程中,弹簧的弹性势能先减小后增大 | ||
| B、小环从A点运动到B点的过程中,小环的电势能一直增大 | ||
C、电场强度的大小E=
| ||
D、小环在A点时受到大环对它的弹力大小F=mg+
|
 如图所示,竖直平面内有一段不光滑的斜直轨道与光滑的圆形轨道相切,切点P与圆心O的连线与竖直方向的夹角为θ=60°,圆形轨道的半径为R,一质量为m的小物块从斜轨道上A点由静止开始下滑,然后沿圆形轨道运动,A点相对圆形轨道底部的高度h=7R,物块通过圆形轨道最高点c时,与轨道间的压力大小为3mg.求:
如图所示,竖直平面内有一段不光滑的斜直轨道与光滑的圆形轨道相切,切点P与圆心O的连线与竖直方向的夹角为θ=60°,圆形轨道的半径为R,一质量为m的小物块从斜轨道上A点由静止开始下滑,然后沿圆形轨道运动,A点相对圆形轨道底部的高度h=7R,物块通过圆形轨道最高点c时,与轨道间的压力大小为3mg.求: 如图所示,竖直平面内的3/4圆弧形光滑轨道ABC,其半径为R,A端与圆心O等高,B为轨道最低点,C为轨道最高点.AE为水平面,一小球从A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达C点.求:
如图所示,竖直平面内的3/4圆弧形光滑轨道ABC,其半径为R,A端与圆心O等高,B为轨道最低点,C为轨道最高点.AE为水平面,一小球从A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达C点.求: 如图所示的竖直平面内有范围足够大,水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B,一绝缘轨道由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP的磁场边界左侧,P、M点在磁场边界线上.现在有一质量为m、带电荷量为+q的中间开孔的小环穿在MN杆上,可沿轨道运动,它所受电场力为重力的
如图所示的竖直平面内有范围足够大,水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B,一绝缘轨道由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP的磁场边界左侧,P、M点在磁场边界线上.现在有一质量为m、带电荷量为+q的中间开孔的小环穿在MN杆上,可沿轨道运动,它所受电场力为重力的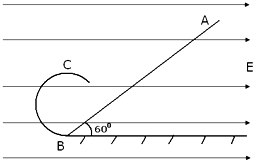 如图所示,竖直平面内的光滑绝缘轨道由斜面部分AB和圆弧部分BC平滑连接,且圆弧轨道半径为R,整个轨道处于水平向右的匀强电场中.一个带正电的小球(视为质点)从斜轨道上某一高度处由静止释放,沿轨道滑下(小球经过B点时无动能损失),已知小球的质量为m,电量为q,电场强度E=
如图所示,竖直平面内的光滑绝缘轨道由斜面部分AB和圆弧部分BC平滑连接,且圆弧轨道半径为R,整个轨道处于水平向右的匀强电场中.一个带正电的小球(视为质点)从斜轨道上某一高度处由静止释放,沿轨道滑下(小球经过B点时无动能损失),已知小球的质量为m,电量为q,电场强度E=