题目内容
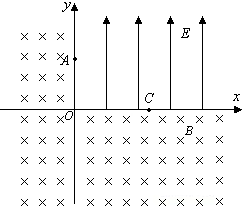 如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀强电场,A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为1.5h.一质量为m、电荷量为q的带负电的粒子以大小为v0的初速度沿x轴方向从A点进入电场区域,继而经过C点离开电场区域.不计重力作用.(sin53?=0.8,cos53?=0.6)
如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀强电场,A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为1.5h.一质量为m、电荷量为q的带负电的粒子以大小为v0的初速度沿x轴方向从A点进入电场区域,继而经过C点离开电场区域.不计重力作用.(sin53?=0.8,cos53?=0.6)(1)求匀强电场的电场强度E.
(2)求粒子经过C点时速度的大小和方向.
分析:(1)带电粒子先在电场中做类平抛运动,后在磁场中偏转,做匀速圆周运动.在电场中,运用运动的分解,根据牛顿第二定律和运动学公式结合求E;
(2)粒子经过C点时速度由水平和竖直两个方向的速度进行合成得到;
(2)粒子经过C点时速度由水平和竖直两个方向的速度进行合成得到;
解答:解:(1)设由A点运动到C点经历的时间为t,则有:1.5h=v0t
以a表示粒子在电场作用下的加速度,有
qE=ma
h=
at2
解得:E=
(2)设粒子从C点进入磁场时的速度为v,v垂直于x 轴的分量
vy=at
则:v=
=
v0
设粒子经过C点时的速度方向与x轴夹角为,则有
cosα=
=
即:α=53°
答:(1)匀强电场的电场强度为
.
(2)粒子经过C点时速度的大小为
v0,x轴夹角为53°.
以a表示粒子在电场作用下的加速度,有
qE=ma
h=
| 1 |
| 2 |
解得:E=
8m
| ||
| 9qh |
(2)设粒子从C点进入磁场时的速度为v,v垂直于x 轴的分量
vy=at
则:v=
|
| 5 |
| 3 |
设粒子经过C点时的速度方向与x轴夹角为,则有
cosα=
| v0 |
| v |
| 3 |
| 5 |
即:α=53°
答:(1)匀强电场的电场强度为
8m
| ||
| 9qh |
(2)粒子经过C点时速度的大小为
| 5 |
| 3 |
点评:本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握平抛运动和圆周运动的基本公式,并几何几何关系解题,难度适中.

练习册系列答案
相关题目
 空间有一匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点(图中未画出)的坐标为 (
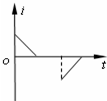
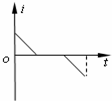
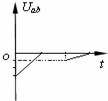
空间有一匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点(图中未画出)的坐标为 (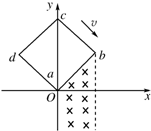 (2011?浙江模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )
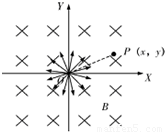
(2011?浙江模拟)如图所示,在坐标系xOy中,有边长为a的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,左边界与y轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )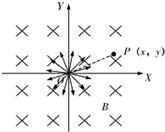 如图所示,在坐标系O-XY平面内的O点,有速率相同、方向各异、质量为m、电量为-q的粒子.匀强磁场的磁感应强度为B,方向垂直纸面向里.坐标系中点P的坐标为P(x,y).不计粒子的重力,不考虑粒子之间的相互作用.下列判断正确的是( )
如图所示,在坐标系O-XY平面内的O点,有速率相同、方向各异、质量为m、电量为-q的粒子.匀强磁场的磁感应强度为B,方向垂直纸面向里.坐标系中点P的坐标为P(x,y).不计粒子的重力,不考虑粒子之间的相互作用.下列判断正确的是( )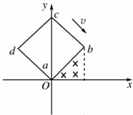 如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )
如图所示,在坐标系xOy中,有边长为L的正方形金属线框abcd,其一条对角线ac和y轴重合、顶点a位于坐标原点O处.在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场,磁场的上边界与线框的ab边刚好完全重合,下边界与x轴重合,右边界与y轴平行.t=0时刻,线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域.取a→b→c→d→a的感应电流方向为正,则在线圈穿越磁场区域的过程中,感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的( )