题目内容
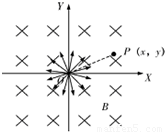
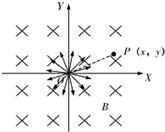如图所示，在坐标系O-XY平面内的O点，有速率相同、方向各异、质量为m、电量为-q的粒子．匀强磁场的磁感应强度为B，方向垂直纸面向里．坐标系中点P的坐标为P（x，y）．不计粒子的重力，不考虑粒子之间的相互作用．下列判断正确的是（ ）分析：带电粒子在匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力，根据圆的对称性，分析可知从O点出发的粒子中，可能有两个出发方向的粒子会过点．知道过P点粒子的出发方向与OP之间的夹角，根据粒子速度的偏向角等于轨迹所对应的圆心角，就能求出圆心角，由几何知识可求出轨迹的半径，由r=
即能求出粒子的运行速度．知道过P点粒子的出发方向与OX轴之间的夹角，由于OP与x轴的夹角可求出，P点粒子的出发方向与OP之间的夹角也可求出，则也可求得粒子的运行速度．
| mv |
| qB |
解答：解：
A、B带电粒子在匀强磁场中做匀速圆周运动，速率大小一定，由r=
得知，粒子运动的半径一定，若r≠
，由几何知识可知，过O、P的圆有两个，粒子的速度也有两个方向．故A错误，B正确．
C、若知道过P点粒子的速度方向与OP之间的夹角，根据粒子速度的偏向角等于轨迹所对应的圆心角，就能求出轨迹的圆心角，OP=
，由几何知识可求出轨迹的半径，由r=
即能求出粒子的运行速度．故C正确．
D、OP与x轴的夹角为arctan
，若知道过P点粒子的出发方向与OX轴之间的夹角，由几何知识可求出P点粒子的速度方向与OP之间的夹角，就能求出速度的偏向角，可求出轨迹的圆心角，OP=
，由几何知识可求出轨迹的半径，由r=
即能求出粒子的运行速度．故D正确．
故选BCD
A、B带电粒子在匀强磁场中做匀速圆周运动，速率大小一定，由r=
| mv |
| qB |
| OP |
| 2 |
C、若知道过P点粒子的速度方向与OP之间的夹角，根据粒子速度的偏向角等于轨迹所对应的圆心角，就能求出轨迹的圆心角，OP=
| x2+y2 |
| mv |
| qB |
D、OP与x轴的夹角为arctan
| y |
| x |
| x2+y2 |
| mv |
| qB |
故选BCD
点评：本题关键抓住粒子速度的偏向角等于轨迹所对应的圆心角进行分析．对于带电粒子在磁场中的匀速圆周运动，要充分利用圆的对称性研究轨迹的特点，由几何知识求解半径，即可求出粒子的速度．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
空间有一匀强电场，在电场中建立如图所示的直角坐标系O-xyz，M、N、P为电场中的三个点，M点的坐标（0，a，0），N点的坐标为（a，0，0），P点（图中未画出）的坐标为 （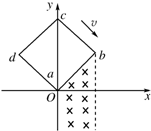
（2011?浙江模拟）如图所示，在坐标系xOy中，有边长为a的正方形金属线框abcd，其一条对角线ac和y轴重合、顶点a位于坐标原点O处．在y轴的右侧的Ⅰ、Ⅳ象限内有一垂直纸面向里的匀强磁场，磁场的上边界与线框的ab边刚好完全重合，左边界与y轴重合，右边界与y轴平行．t=0时刻，线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域．取沿a→b→c→d→a的感应电流方向为正，则在线圈穿越磁场区域的过程中，感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的（ ）
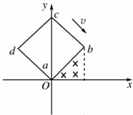如图所示，在坐标系xOy中，有边长为L的正方形金属线框abcd，其一条对角线ac和y轴重合、顶点a位于坐标原点O处．在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场，磁场的上边界与线框的ab边刚好完全重合，下边界与x轴重合，右边界与y轴平行．t=0时刻，线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域．取a→b→c→d→a的感应电流方向为正，则在线圈穿越磁场区域的过程中，感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的（ ）
