Question

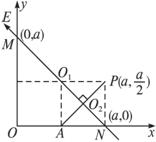
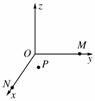
空间有一匀强电场，在电场中建立如图所示的直角坐标系O-xyz，M、N、P为电场中的三个点，M点的坐标（0，a，0），N点的坐标为（a，0，0），P点（图中未画出）的坐标为 （

a

2

，a，

a

2

）．已知电场方向平行于直线MN，M点电势为0，N点电势为1V，则P点的电势为：（　　）

• A．

  2

  2

  V
• B．

  3

  2

  V
• C．

  1

  4

• D．

  3

  4

  V

Answer 1

分析：将电场强度沿坐标轴方向正交分解，求出轴向的E的分量值，再选用U=Ed，求得电势差，得电势．

解答：解：根据题意已知电场方向平行于直线MN，点M的电势为0，点N的电势为1V，故
      U_NM=E?

2

a=1V          ①
将电场强度沿着-x方向和+y方向正交分解，设合场强为E，则-x和+y方向的分量分别为：
     E_x=

2

2

E，E_y=

2

2

E    ②
   设P在x0y平面上的投影为P′点，投影点的坐标为：（

a

2

，a，0）
  则 U_MP=U_MP′=E_y?a

1

2

=

1

4

V   （由①②式得）
   又M点电势为0，则P′点势为

1

4

V，即P点电势为

1

4

V
  则 A B D错误，C正确
故选：C

点评：本题关键运用正交分解法，将电场沿着坐标轴方向正交分解，然后由U=Ed求解．