题目内容
20.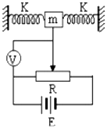 如图所示为一种加速度仪的示意图.质量为 m 的振子两端连有劲度系数均为 k 的轻弹簧,电源的电动势为 E,不计内阻,滑动变阻器的总阻值为 R,有效长度为 L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.
如图所示为一种加速度仪的示意图.质量为 m 的振子两端连有劲度系数均为 k 的轻弹簧,电源的电动势为 E,不计内阻,滑动变阻器的总阻值为 R,有效长度为 L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.(1)系统的加速度a(以向右为正)和电压表读数U的函数关系式a=$\frac{kL}{mE}$(E-2U).
(2)若电压表指针指在满刻度的$\frac{3}{4}$位置,此时系统的加速度大小为$\frac{kL}{2mE}$和方向向左(填“左”或“右”)
分析 (1)根据牛顿第二定律和胡克定律求出加速度与振子偏离变阻器中点的距离的关系式.根据欧姆定律和电阻定律求出电压表读数U与振子偏离变阻器中点的距离的关系式,再综合得出系统的加速度a和电压表读数U的函数关系式.
(2)当变阻器触片滑到最右端时电压表的读数等于电源的电动势,得到电压表指针指在满刻度的$\frac{3}{4}$位置时电压值,代入加速度的表达式,求出加速度.
解答 解:(1)当振子向左偏离变阻器中间位置x距离时,对振子,根据牛顿第二定律得:
2kx=ma…①
根据欧姆定律和串联电路分压特点得:
U=$\frac{\frac{L}{2}-x}{L}$E…②
联立①②得:a=$\frac{kL}{mE}$(E-2U)
(2)由加速度的表达式可知,a与U是线性关系,所以加速度仪的刻度盘是均匀的,当变阻器触片滑到最右端时电压表的读数等于电源的电动势E,得到电压表指针指在满刻度的$\frac{3}{4}$位置时电压值为:U=$\frac{3}{4}$E.
代入到加速度a的表达式得:a=-$\frac{kL}{2mE}$,负号表示方向向左.
故答案为:(1)a=$\frac{kL}{mE}$(E-2U).(2)$\frac{kL}{2mE}$;左.
点评 本题是力电综合题,寻找力与电联系的纽带是关系,此题力电联系的纽带是振子的位移.

练习册系列答案
相关题目
11.法拉第电磁感应定律可以这样表述:闭合电路中的感应电动势的大小( )
| A. | 跟穿过这一闭合电路的磁通量成正比 | |
| B. | 跟穿过这一闭合电路的磁通量的变化量成正比 | |
| C. | 跟穿过这一闭合电路的磁通量的变化率成正比 | |
| D. | 跟穿过这一闭合电路的磁感应强度成正比 |
15. 如图所示电路可用来测定电池组的电动势和内电阻.其中V为电压表(其电阻足够大),定值电阻R=7.0Ω.在电键未接通时,V的读数为6.0V;接通电键后,V的读数变为5.6V.那么,电池组的电动势和内电阻分别等于( )
如图所示电路可用来测定电池组的电动势和内电阻.其中V为电压表(其电阻足够大),定值电阻R=7.0Ω.在电键未接通时,V的读数为6.0V;接通电键后,V的读数变为5.6V.那么,电池组的电动势和内电阻分别等于( )
 如图所示电路可用来测定电池组的电动势和内电阻.其中V为电压表(其电阻足够大),定值电阻R=7.0Ω.在电键未接通时,V的读数为6.0V;接通电键后,V的读数变为5.6V.那么,电池组的电动势和内电阻分别等于( )
如图所示电路可用来测定电池组的电动势和内电阻.其中V为电压表(其电阻足够大),定值电阻R=7.0Ω.在电键未接通时,V的读数为6.0V;接通电键后,V的读数变为5.6V.那么,电池组的电动势和内电阻分别等于( )| A. | 6.0 V,0.5Ω | B. | 6.0 V,1.25Ω | C. | 5.6 V,1.25Ω | D. | 5.6 V,0.5Ω |
12.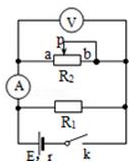 如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
 如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )
如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻,E为电源电动势,r为电源内阻,大小为r=R1,当R2的滑臂P从a滑向b的过程中,下列说法中正确的是( )| A. | 当R2=$\frac{{R}_{1}}{2}$时,R2上获得最大功率 | |
| B. | 当R2=R1时,R2上获得最大功率 | |
| C. | 电压表示数和电流表示数之比逐渐增大 | |
| D. | 电压表示数和电流表示数之比保持不变 |
9.下列说法正确的是( )
| A. | 牛顿通过理想斜面实验总结出力是改变物体运动状态的原因 | |
| B. | 开普勒用20年的时间研究第谷的行星观测记录,总结出了开普行星运动定律 | |
| C. | 第2s末到第4s初的时间间隔是1s | |
| D. | 物体在力的作用下形状或体积发生的改变,叫做弹性形变 |
10. 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )| A. | 电阻R消耗的电功率增大 | B. | 灯L1、L2都能正常发光 | ||
| C. | 原线圈的输入功率减小 | D. | 原、副线圈的电流比减小 |
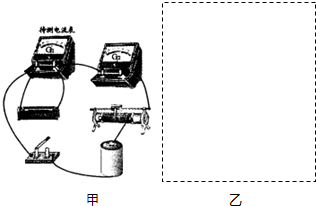 某学习小组利用如图所示的实验电路来测量实际电流表G1的内阻r1的大小.按要求需测量尽量准确,且滑动变阻器调节方便.
某学习小组利用如图所示的实验电路来测量实际电流表G1的内阻r1的大小.按要求需测量尽量准确,且滑动变阻器调节方便.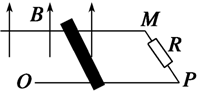 某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.
某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.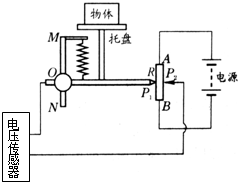 如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx:
如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx: