题目内容
如图所示，半径R=0.40m的半圆轨道处于竖直平面内，半圆与水平地面切于圆的端点A，一质量为m=0.10kg的小球，以一定的初速度水平地面上向左运动后，恰好能到达半圆轨道的最高点B点，最后小球落在C点．（取重力加速度g=10m/s2）．
求（1）小球到达B点的速度是多少？
（2）A、C间的距离有多大．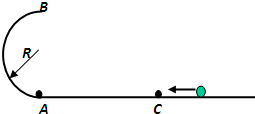
求（1）小球到达B点的速度是多少？
（2）A、C间的距离有多大．
（1）小球恰好能到达半圆轨道的最高点B点，说明小球在B点只受重力，根据牛顿第二定律得
mg=
小球到达B点的速度vB=
=2m/s．
（2）小球能够到达B点，且从B点作平抛运动，
在竖直方向有
2R=
gt2
在水平方向有
sAC=vBt
解得：sAC=0.8m
答：（1）小球到达B点的速度是2m/s
（2）A、C间的距离是0.8m．
mg=
| ||
| R |
小球到达B点的速度vB=
| gR |
（2）小球能够到达B点，且从B点作平抛运动，
在竖直方向有
2R=
| 1 |
| 2 |
在水平方向有
sAC=vBt
解得：sAC=0.8m
答：（1）小球到达B点的速度是2m/s
（2）A、C间的距离是0.8m．
练习册系列答案
53随堂测系列答案
相关题目
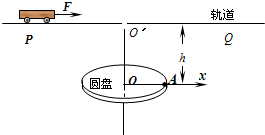（2011?淮安三模）如图所示，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点．一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=2m处由静止开始沿轨道向右运动，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合．规定经过O点水平向右为x轴正方向．小车与轨道间的动摩擦因数μ=0.2，g取10m/s2．求：
（2005?广东）如图所示，半径R=0.40m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A．一质量m=0.10kg的小球，以初速度v0=7.0m/s在水平地面上向左作加速度a=3.0m/s2的匀减速直线运动，运动4.0m后，冲上竖直半圆环，最后小球落在C点．求A、C间的距离（取重力加速度g=10m/s2）．
如图所示，半径R=0.8m的四分之一光滑圆弧轨道竖直固定，轨道末端水平，其右方有横截面半径r=0.2m的转筒，转筒顶端与轨道最低点B等高，下部有一小孔，距 顶端h=0.8m，转筒的轴线与圆弧轨道在同一竖直平面内，开始时小孔也在这一平面内的图示位置．现使一质量m=0.1kg的小物块自最高点A由静止开始沿圆弧轨道滑下，到达轨道最低点B时转筒立刻以某一角速度匀速转动起来，且小物块最终正好进入小孔．不计空气阻力，g取l0m/s2，求：
如图所示，半径r=0.8m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一质量为0.4kg的小球（小球的半径比r小很多）．现给小球一个水平向右的初速度v0，下列关于在小球的运动过程中说法正确的是（g取10m/s2）（ ）| A、v0≤4m/s可以使小球不脱离轨道 | ||
B、v0≥4
| ||
| C、设小球能在圆轨道中做完整的圆周运动，在最低点与最高点对轨道的压力之差为24N | ||
| D、设小球能在圆轨道中做完整的圆周运动，在最低点与最高点对轨道的压力之差为20N |
如图所示，半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点，O为圆弧圆心，D为圆弧最低点，斜面体ABC固定在地面上，顶端B安装一定滑轮，一轻质软细绳跨过定滑轮（不计滑轮摩擦）分别连接小物块P、Q（两边细绳分别与对应斜面平行），并保持P、Q两物块静止．若PC间距为L1=0.25m，斜面MN粗糙且足够长，物块P质量m1=3kg，与MN间的动摩擦因数μ=