题目内容
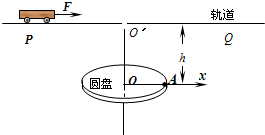 (2011?淮安三模)如图所示,半径R=0.4m的圆盘水平放置,绕竖直轴OO′匀速转动,在圆心O正上方h=0.8m高处固定一水平轨道PQ,转轴和水平轨道交于O′点.一质量m=1kg的小车(可视为质点),在F=4N的水平恒力作用下,从O′左侧x0=2m处由静止开始沿轨道向右运动,当小车运动到O′点时,从小车上自由释放一小球,此时圆盘半径OA与x轴重合.规定经过O点水平向右为x轴正方向.小车与轨道间的动摩擦因数μ=0.2,g取10m/s2.求:
(2011?淮安三模)如图所示,半径R=0.4m的圆盘水平放置,绕竖直轴OO′匀速转动,在圆心O正上方h=0.8m高处固定一水平轨道PQ,转轴和水平轨道交于O′点.一质量m=1kg的小车(可视为质点),在F=4N的水平恒力作用下,从O′左侧x0=2m处由静止开始沿轨道向右运动,当小车运动到O′点时,从小车上自由释放一小球,此时圆盘半径OA与x轴重合.规定经过O点水平向右为x轴正方向.小车与轨道间的动摩擦因数μ=0.2,g取10m/s2.求:(1)若小球刚好落到A点,求小车运动到O′点的速度.
(2)为使小球刚好落在A点,圆盘转动的角速度应为多大.
(3)为使小球能落到圆盘上,求水平拉力F作用的距离范围.
分析:(1)物块离开O′点后做平抛运动,可以求出平抛运动的时间和平抛运动的初速度,从而得出小车运动到O′点速度(2)若圆盘转一圈,物块恰好调入小桶,此时作用力时间最短.圆盘转一圈的时间与平抛运动时间是相等.从而得出圆盘转动的角速度最小值.也有可能在平抛运动时间内,圆盘转动N圈.因此求出转动角速度.
(3)小球能落在圆盘上,则可利用平抛运动,可求出小球抛出的速度范围,从而得出小球的加速度的范围.最终运用牛顿第二定律可求出水平拉力的距离范围.
(3)小球能落在圆盘上,则可利用平抛运动,可求出小球抛出的速度范围,从而得出小球的加速度的范围.最终运用牛顿第二定律可求出水平拉力的距离范围.
解答:解:(1)小球离开小车后,由于惯性,将以离开小车时的速度作平抛运动,h=
gt2
R=vt
小车运动到O′点的速度v=
=1m/s
(2)为使小球刚好落在A点,则小球下落的时间为圆盘转动周期的整数倍,有t=kT=
,其中k=1,2,3…
即ω=2kπ
=5kπrad/s,其中k=1,2,3…
(3)小球若能落到圆盘上,其在O′点的速度范围是:0<v≤1m/s
设水平拉力作用的最小距离与最大距离分别为x1、x2,对应到达O′点的速度分别为0、1m/s.
由动能定理,有 Fx1-μmgx0=0
代入数据解得x1=1m
根据动能定理,有 Fx2-μmgx0=
mv2-0
代入数据解得x2=1.125m或
m
则水平拉力F作用的距离范围 1m<x≤1.125m
答:(1)若小球刚好落到A点,求小车运动到O′点的速度1m/s.
(2)为使小球刚好落在A点,圆盘转动的角速度应为ω=2kπ
=5kπrad/s,其中k=0,1,2,3…
(3)为使小球能落到圆盘上,求水平拉力F作用的距离范围 1m<x≤1.125m
| 1 |
| 2 |
R=vt
小车运动到O′点的速度v=
| R |
| t |
(2)为使小球刚好落在A点,则小球下落的时间为圆盘转动周期的整数倍,有t=kT=
| 2kπ |
| ω |
即ω=2kπ
|
(3)小球若能落到圆盘上,其在O′点的速度范围是:0<v≤1m/s
设水平拉力作用的最小距离与最大距离分别为x1、x2,对应到达O′点的速度分别为0、1m/s.
由动能定理,有 Fx1-μmgx0=0
代入数据解得x1=1m
根据动能定理,有 Fx2-μmgx0=
| 1 |
| 2 |
代入数据解得x2=1.125m或
| 9 |
| 8 |
则水平拉力F作用的距离范围 1m<x≤1.125m
答:(1)若小球刚好落到A点,求小车运动到O′点的速度1m/s.
(2)为使小球刚好落在A点,圆盘转动的角速度应为ω=2kπ
|
(3)为使小球能落到圆盘上,求水平拉力F作用的距离范围 1m<x≤1.125m
点评:解决本题的关键知道物块整个过程的运动:匀加速直线运动、匀减速直线运动和平抛运动,知道三个过程的运动时间与圆盘转动的时间相等.以及熟练运用运动学公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2011?淮安三模)闭合矩形导线框abcd固定在匀强磁场中,磁场的方向与导线框所在平面垂直,磁感应强度B随时间t变化的规律如图所示.规定垂直纸面向里为磁场的正方向,abcda的方向为线框中感应电流的正方向,水平向右为安培力的正方向.关于线框中的电流i与ad边所受的安培力F随时间t变化的图象,下列正确的是( )
(2011?淮安三模)闭合矩形导线框abcd固定在匀强磁场中,磁场的方向与导线框所在平面垂直,磁感应强度B随时间t变化的规律如图所示.规定垂直纸面向里为磁场的正方向,abcda的方向为线框中感应电流的正方向,水平向右为安培力的正方向.关于线框中的电流i与ad边所受的安培力F随时间t变化的图象,下列正确的是( ) (2011?淮安三模)真空中有一半径为r0的带电金属球壳,通过其球心的一直线上各点的电势φ分布如图,r表示该直线上某点到球心的距离,r1、r2分别是该直线上A、B两点离球心的距离.下列说法中正确的是( )
(2011?淮安三模)真空中有一半径为r0的带电金属球壳,通过其球心的一直线上各点的电势φ分布如图,r表示该直线上某点到球心的距离,r1、r2分别是该直线上A、B两点离球心的距离.下列说法中正确的是( )