题目内容

【题目】如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直．一质量为m、电荷量为﹣q（q＞0）的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场．粒子在磁场中的运动轨迹与y轴交于M点．已知OP=l，OQ=2l．不计重力．求：

（1）M点与坐标原点O间的距离；

（2）粒子从P点运动到M点所用的时间．

【答案】（1）6L；（2）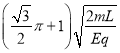

【解析】（1）带电粒子在电场中做类平抛运动，在y轴负方向上做初速度为零的匀加速运动，设加速度的大小为a；在x轴正方向上做匀速直线运动，设速度为v0；粒子从P点运动到Q点所用的时间为t1，进入磁场时速度方向与x轴正方向的夹角为θ，则

由牛顿第二定律得：qE=ma①

在电场中运动的时间为： ②

水平初速度： ③

其中 ，y0=L，又 ④

联立②③④得θ=30°⑤

由几何关系知MQ为直径， ⑥

MO==6L ⑦

（2）设粒子在磁场中运动的速度为v，从Q到M点运动的时间为t2，则有

⑧

⑨

从P点到M点所用的时间t=t1+t2⑩

联立①②③⑤⑥⑧⑨⑩并代入数据得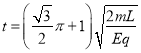

练习册系列答案
相关题目

【题目】（1）为进行“验证机械能守恒定律”的实验，有下列器材可供选择：

A、铁架台

B、电火花打点计时器

C、墨盘

D、纸带

E、重锤

F、天平

G、秒表

H、220V交流电

上述器材不必要的是_____（只填字母代号），缺少的器材是_____．

（2）在做“验证机械能守恒定律”的实验时，用打点计时器打出纸带如图所示，其中A点为打下的第一个点．其中A点为打下的第一个点，0、1、2…为连续的计数点．现测得两相邻计数点之间的距离分别为s1、s2、s3、s4、s5、s6，已知计数点间的时间间隔均为T．根据纸带测量出的距离及打点的时间间隔，可以求出次实验过程中重锤下落运动的加速度大小表达式为_____，在打下第5号计数点时，纸带运动的瞬时速度大小的表达式为_____．要验证机械能守恒定律，为减小实验误差，应选择打下第_____号和第___ 　号计数点之间的过程为研究对象．

【题目】在测量金属丝电阻率的实验中，可供选用的器材如下：

待测金属丝：Rx(阻值约4 Ω)；

电压表：(量程3 V，内阻约3 kΩ)；

电流表：A1(量程0.6 A，内阻约0.2 Ω)，

A2：(量程3 A，内阻约0.05 Ω)；

电源：E1(电动势3 V，内阻不计)，

E2：(电动势12 V，内阻不计)；

滑动变阻器：R(最大阻值约20 Ω)；

螺旋测微器：毫米刻度尺；开关S；导线。

（1）用螺旋测微器测量金属丝的直径，示数如图所示，读数为________mm。

（2）若滑动变阻器采用限流接法，为使测量尽量精确，电流表应选________，电源应选________(均填器材代号)。

（3）在答题纸对应题号线框内完成电路原理图__________。

【题目】2017年4月22日12时23分，天舟一号货运飞船与天宫二号空间实验室顺利完成自动交会对接。已知天宫二号距离地面的高度为。下列关于它们的运动的说法正确的是（ ）

A. 天舟一号的发射速度应小于

B. 天舟一号与天宫二号对接前在较低的轨道上做匀速圆周运动的周期小于天宫二号运行的周期

C. 天舟一号与天宫二号对接前在较低的轨道上做匀速圆周运动的线速度应小于天宫二号的线速度

D. 天舟一号与天宫二号对接后，天宫二号的速度将增加，从而降低到更低的轨道

【题目】某静电场方向平行于x轴，其电势φ随x变化规律如图所示。一质量为m、带电量为＋q的粒子(不计重力)，以初速度v0从O点(x＝0)进入电场，仅在电场力的作用下沿x轴正方向运动。下列说法正确的是(　　)

A. 粒子从O运动到x1的过程中做匀加速直线运动

B. 粒子从x1运动到x3的过程中，电势能一直减少

C. 若v0为 ，带电粒子在运动过程中的最大速度为

D. 若使粒子能运动到x4处，则初速度v0至少为

【题目】如图电路中，电源的内电阻为r，R1、R3、R4均为定值电阻，电表均为理想电表。闭合电键S，当滑动变阻器R2的滑动触头向右滑动时，下列说法中正确的是( )

A. 电压表的示数变小

B. 电流表的示数变小

C. R1中电流的变化量一定大于R4中电流的变化量

D. 电压表示数的变化量与电流表示数的变化量之比一定小于电源的内电阻r

【题目】公交给居民出行带来了方便，很多城市都建设了公交专线。如图所示，公路上有一辆公共汽车以的速度匀速行驶，为了平稳停靠在站台，在距离站台左侧位置处开始刹车做匀减速直线运动。公交车刚刹车时，一乘客为了搭车，从距站台右侧处由静止正对着站台跑去，人先做匀加速直线运动，速度达到后匀速运动一段时间，接着做匀减速直线运动，最终人和和同时到达站台停下，乘客顺利上车。人加速和减速的加速度大小相等。求：（不考虑站台大小和公交车的大小）

（1）公交车刹车的加速度大小；

（2）人的加速度的大小。

【题目】跳台滑雪运动员的动作惊险而优美，其实滑雪运动可抽象为物体在斜坡上的平抛运动。如图所示，设可视为质点的滑雪运动员，从倾角为θ的斜坡顶端P处，以初速度水平飞出，最后又落到斜坡上A点处，AP之间距离为L，在空中运动时间为t。改变运动员初速度的大小，L和t都随之改变.关于L、t与的关系，下列说法中正确的是

A. t与成反比 B. t与成正比

C. L与成正比 D. L与成正比

【题目】某同学设计了如甲、乙两图所示的实验装置来探究加速度与物体质 量、物体受力的关系。

（1）（填“甲”或“乙”）_______实验装置比较好，原因是_______

（2）该同学选择比较理想的实验装置后，平衡摩擦力后，打出了一条纸带如图 丙所示，计时器打点的时间间隔为 0.02s．从比较清晰的点起，每5个点取一个 计数点，量出相邻计数点之间的距离，该小车经过计数点“2” 的瞬时速度 v=_____m/s，加速度 a=_______________ m/s2 （结果保留两位有效数字）

（3）在实验误差允许范围内，当小车的质量不变时，小车的加速度与小车的合 外力满足图_______的关系。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网